离散数学2008年7月考试真题(02324)
-
在某次国际会议的预备会中,共有8人参加,他们来自不同的国家。已知他们中任何两个无共同语言的人中的每一个,与其余有共同语言的人数之和大于或等于8,问能否将这8个人排在圆桌旁,使其任何人都能与两边的人交谈。
-
构造下面推理的证明。只要A曾到过受害者房间并且11点以前没离开,A就犯了谋杀罪。A曾到过受害者房间。如果在11点以前离开,看门人会看见他。看门人没有看见他。所以A犯了谋杀罪。
-
简单图G有n个结点,m条边,设m>(n-1)(n-2)/2,证明:G是连通的。
-
设H是形如
 的2×2阶矩阵的集合,H中定义通常的矩阵乘法运算。验证H是群,
的2×2阶矩阵的集合,H中定义通常的矩阵乘法运算。验证H是群,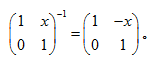 。
。 -
设R为N×N上的二元关系
 证明R为等价关系。
证明R为等价关系。 -
设A={a,b,c},P(A)是A的幂集,R为A上的包含关系,试给出的哈斯图,并给出子集{{a,b},{a,c},{c}}的极大元、极小元、最大元、最小元。
-
设X={1,2,3,4},R是X上的二元关系,R={<1,1>,<3,1>,<1,3>,<3,3>,<3,2>,<4,3>,<4,1>,<4,2>,<1,2>}。
(1)画出R的关系图;
(2)写出R的关系矩阵;
(3)说明R是否具有自反、反自反、对称、传递性质。
-
求下列公式的主析取范式和主合取范式:
 。
。 -
构造命题公式
 的真值表。
的真值表。 -
若集合A={1,{2,3}}的幂集为P(A),集合B={{
 ,2},{2}}的幂集为P(B),求P(A)∩ P(B)。
,2},{2}}的幂集为P(B),求P(A)∩ P(B)。
2018年4月电子商务全国自考(电子
2017年10月电子商务全国自考(电
2017年4月电子商务全国自考(电子
2016年10月电子商务全国自考(电
2016年4月电子商务全国自考(电子
2015年10月电子商务全国自考(电
2015年4月电子商务全国自考(电子
2014年10月电子商务全国自考(电
2014年4月电子商务全国自考(电子
2013年10月电子商务全国自考(电
 的2×2阶矩阵的集合,H中定义通常的矩阵乘法运算。验证H是群,
的2×2阶矩阵的集合,H中定义通常的矩阵乘法运算。验证H是群,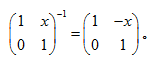 。
。