离散数学2008年4月考试真题（02324）

今要将6人分成3组(每组2个人)去完成3项任务。已知每个人至少与其余5个人中的3个人能相互合作。

(1)能否使得每组的2个人都能相互合作?

(2)你能给出几种不同的分组方案?

构造下面推理的证明。

每个喜欢步行的人都不喜欢坐汽车，每个人或者喜欢坐汽车或者喜欢骑自行车。有的人不喜欢骑自行车，因而有的人不喜欢步行。

设R是A上的自反和传递关系，如下定义A上的关系T，使得

证明：T是A上的等价关系。

设有G=，V的结点数|V|=n，称该图为n阶图，若从结点v_i到v_j存在路，证明：从vi到v_j必存在长度小于等于n-1的一条路。

给定图G如图所示，

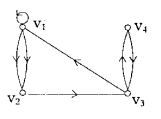
(1)G中长度为4的路有几条?其中有几条回路?

(2)写出G的可达矩阵。

设(L，≤)是格，试证明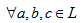：, 有a∧(b∨c)≥(a∧b)∨(a∧c);　a∨(b∧c)≤(a∨b)∧(a∨c)。

设A={a, b, c, d, e}，R为A上的关系，R={，，, , 　　e>,, }∪IA，试画的哈斯图，并求A中的最大元，最小元，极大元，　　极小元。

构造命题公式的真值表。

求下列公式的主析取范式和主合取范式：

设A={a，b，c，d}，A上的等价关系∪IA，画出R的关系图，并求出A中各元素的等价类。