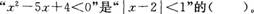2014年教师资格考试《中学数学学科知识与教学能力》专家预测试卷(5)
-
请以“三角形相似(第二课时)”为课题,完成下列教学设计。(1)教学目标;(2)教学重点、难点;(3)教学过程(只要求写出新课导人和新知探究、巩固和应用)。
-
根据以下案例,回答后面的问题。
教学过程:
习旧引新
(1)在⊙O上,任取三个点A、B、C,然后顺次连接,得到的是什么图形?这个图形与⊙O有什么关系?
(2)由圆内接三角形的概念,能否得出什么是圆的内接四边形呢(类比)?
概念学习
(1)什么叫圆的内接四边形?
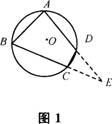
(2)如图1,说明四边形ABCD与⊙O的关系。
探讨性质
(1)前面我们已经学习了一类特殊四边形——平行四边形,矩形,菱形,正方形,等腰梯形的性质,那么要探讨圆内接四边形的性质,一般要从哪几个方面入手?
(2)打开《几何画板》,让学生动手任意画⊙O和⊙O的内接四边形ABCD。(教师适当指导)
(3)量出所有值(圆的半径和四边形的边,内角,对角线,周长,面积),并观察这些量之间的关系。
(4)改变圆的半径大小,这些量有无变化?由(3)观察得出的某些关系有无变化?
(5)移动四边形的一个顶点,这些量有无变化?由(3)观察得出的某些关系有无变化?移动四边形的四个顶点呢?移动三个顶点呢?
(6)如何用命题的形式表述刚才的实验得出来的结论呢?(让学生回答)
性质的证明及巩固练习
(1)证明猜想
(2)完善性质
①若将线段BC延长到E,那么,∠DCE与∠BAD又有什么关系呢?
②圆的内接四边形的性质定理:圆内接四边形的对角互补,并且任何一个外角都等于它的内对角。
(3)练习。
例题讲解
小结:为了使学生对所学的内容有一个完整而深刻的印象,让学生组成小组,从概念,性质,方法,特殊性进行讨论,然后对讨论的结果进行归纳。
(1)本节课我们学习了圆内接四边形的概念及圆内接四边形的主要性质,要求同学们理解圆
内接四边形和四边形的外接圆的概念,理解圆内接四边形的性质定理,并初步应用性质定理进行有关命题的证明和计算。
(2)我们结合《几何画板》的使用导出了圆内接四边形的性质,在这一过程中用到了许多数学方法(实验,观察,类比,分析,归纳,猜想等),同学们要逐步学会并应用这些方法去探讨有关的数学问题,提高我们的数学实践能力与创新能力。
问题:(1)一般数学概念的学习包括哪几个方面的内容?
(2)概念的获取一般有哪些形式?
(3)谈谈你对该案例的看法。
-
简述数学课程与教学的总体要求及其含义。
-
-

-
简述教学评价的功能。
-
结合实际,你认为一堂好的数学课应符合那些基本要求?
-
课程标准的教学建议有哪七个方面?
-
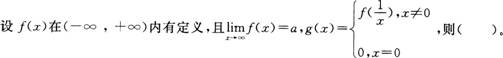
- A.x=0必是g(x)的第一类间断点
- B.x=0必是g(x)的第二类间断点
- C.x=0必是g(x)的连续点
- D.g(x)在点x=0处的连续性与a的取值有关
-
《义务教育数学课程标准(2011年版)》提出了与内容有关的哪10个核心概念?
-
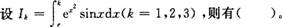
- A.I1<;I2<;I3
- B.I3<;I2<;I1
- C.I2<;I3<;I1
- D.I2<;I1<;I3
-
甲、乙两人玩猜数字游戏,先由甲心中想一个数字,记为a,再由乙猜甲刚才所想的数字,把乙猜的数字记为b,其中a,b∈{1,2,3,4,5,6},若| a-b |≤1,就称甲乙“心有灵犀”。现任意找两人玩这个游戏,则他们“心有灵犀”的概率为( )。
- A.1/9
- B.2/9
- C.7/8
- D.4/9
-
在“数与代数”的教学中,应帮助学生( )。①建立数感②符号意识③发展运算能力和推理能力④初步形成模型思想
- A.①②③
- B.①②④
- C.②③④
- D.①②③④
-
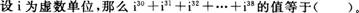
- A.-1
- B.i
- C.-i
-
 A.2
A.2- A.
2
- B.
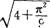
- C.
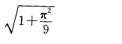
- D.
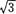
- A.A
- B.B
- C.C
- D.D
- A.
-
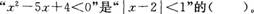
- A.充分不必要条件
- B.必要不充分条件
- C.充要条件
- D.既不充分也不必要条件
-
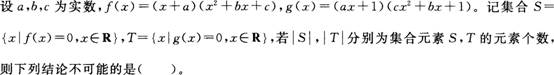
- A.| S |=1且| T|=0
- B.| S |=1且| T |=1
- C.| S |=2且| T |=2
- D.| S |=2且| T |=3

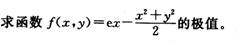

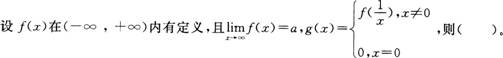
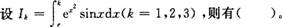
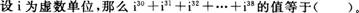
 A.2
A.2