2012年下半年软考《程序员》下午试卷(参考答案版)
-
试题六(共15分)
阅读以下说明和Java程序,填充程序中的空缺,将解答填入答题纸的对应栏内。
【说明】
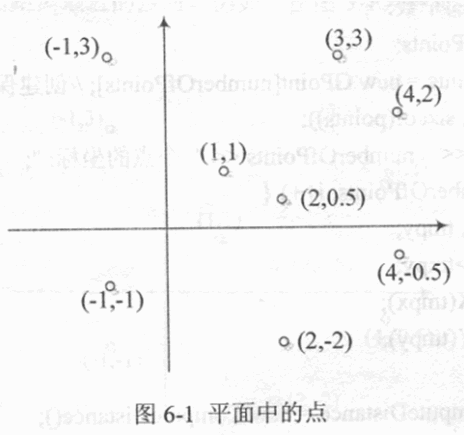
下面的程序用来计算并寻找平面坐标系中给定点中最近的点对(若存在多对,则输出其中的一对即可)。程序运行时,先输入点的个数和一组互异的点的坐标,通过计算每对点之间的距离,从而确定出距离最近的点对。例如,在图6—1所示的8个点中,点(1,1)与(2,0.5)是间距最近的点对。
【Java代码】
import java.util.Scanner;
class GPoint
{
private double x,y;
public void setX(aouble x) {this.x = x;}
public void setY(double y) {this.y = y;)
public double getX() {return this.x;)
public double getY() {return this.y;
}
class FindNearestPoints{
public static void main(String[] args){
Scanner input= new Scanner(System.in);
System.out.print("输入点的个数:");
int numberOfPoints= input.nextlnt();
(1) points= new GPoint[numberOfPoints]; //创建保存点坐标的数组
System.out.print("请输入"+numberOfPoints+"个点的坐标");
for (int i=0;i
points[i]= (2) ;
points[i].setX(input.nextDouble());
points[i].setY(input.nextDouble());
}
FindNearestPoints fnp= new FindNearestPoints();
int p1=0,p2=1; //p1和p2用于表示距离最近的点对在数组中的下标
double shortestDistance=fnp.getDistance(points[p1], points[p2]);
//计算每一对点之间的距离
for (int i=0;i
{
for (intj = 1+1;j< (3) ;j++)
{
double tmpDistance=fnp.(4);
//计算两点间的距离
if( (5) )
{
p1=i;
p2 =j;
shortestDistance = tmpDistance;
}
}
}
System.out.println("距离最近的点对是("+
points[p1].getX()+","+points[p1].getY()+")和(”+
points[p2].getX()+”,”+points[p2].getY()+”)”);
}
public double getDistance(GPoint pt1, GPoint pt2)
{
retum Math.sqrt((pt2.getX() – pt1.getX())*(pt2.getX() – ptl1getX())
+ (pt2.getY() – pt1.getY())*(pt2.getY() – pt1.getY());
}
}
-
试题三(共15分)
阅读以下说明和C函数,填充函数中的空缺,将解答填入答题纸的对应栏内。
【说明】
函数Insert _key (*root,key)的功能是将键值key插入到*root指向根结点的二叉查找树中(二叉查找树为空时*root为空指针)。若给定的二叉查找树中已经包含键值为key的结点,则不进行插入操作并返回0;否则申请新结点、存入key的值并将新结点加入树中,返回l。
提示:
二叉查找树又称为二叉排序树,它或者是一棵空树,或者是具有如下性质的二叉树:
●若它的左子树非空,则其左子树上所有结点的键值均小于根结点的键值;
●若它的右子树非空,则其右子树上所有结点的键值均大于根结点的键值;
●左、右子树本身就是二叉查找树。
设二叉查找树采用二叉链表存储结构,链表结点类型定义如下:
typedef struct BiTnode{
int key _value; /*结点的键值,为非负整数*/
struct BiTnode *left,*right; /*结点的左、右子树指针*/
}BiTnode, *BSTree;
【C函数】
int Insert _key( BSTree *root,int key)
{
BiTnode *father= NULL,*p=*root, *s;
while( (1)&&key!=p->key_value){/*查找键值为key的结点*/
father=p;
if(key< p->key_value)p= (2) ; /*进入左子树*/
else p= (3) ; /木进入右子树*/
}
if (p) return 0; /*二叉查找树中已存在键值为key的结点,无需再插入*/
s= (BiTnode *)malloc( (4) );/*根据结点类型生成新结点*/
if (!s) return -1;
s->key_value= key; s->left= NULL; s->right= NULL;
if( !father)
(5) ; /*新结点作为二叉查找树的根结点*/
else /*新结点插入二叉查找树的适当位置*/
if( key< father->key_value)father->left = s;
elsefather->right = s;
retum 1:
}
-
试题四(共15分)
阅读以下说明和C函数,填充函数中的空缺,将解答填入答题纸的对应栏内。
【说明】
已知两个整数数组A和B中分别存放了长度为m和n的两个非递减有序序列,函数Adjustment(A,B,m,n)的功能是合并两个非递减序列,并将序列的前m个整数存入A中,其余元素依序存入B中。

合并过程如下:从数组A的第一个元素开始处理。用数组B的最小元素B[0]与数组A的当前元素比较,若A的元素较小,则继续考查A的下一个元素;否则,先将A的最大元素暂存入temp,然后移动A中的元素挪出空闲单元并将B[0]插入数组A,最后将暂存在temp中的数据插入数组B的适当位置(保持B的有序性)。如此重复,直到A中所有元素都不大于B中所有元素为止。
【C函数】
void Adjustment(int A[],int B[],int m,int n)
{ /*数组A有m个元素,数组B有n个元素*/
inti,k,temp;
for(i=0;i
{
if(A[i]<=B[0]) continue,
temp= (1) ;/*将A中的最大元素备份至temp*/
/*从后往前依次考查A的元素,移动A的元素并将来自B的最小元素插入A中*/
for(k= m-1; (2) ;k--)
A[k]=A[k-1];
A[i]=(3) ;
/*将备份在temp的数据插入数组B的适当位置*/
for(k=1; (4) &&k
B[k_1]=B[k];
B[k-1]= (5) ;
}
}
-
试题五(共15分)
阅读以下说明和C++代码,填充代码中的空缺,将解答填入答题纸的对应栏内。
【说明】
下面的程序用来计算并寻找平面坐标系中给定点中最近的点对(若存在多对,则输出其中的一对即可)。程序运行时,先输入点的个数和一组互异的点的坐标,通过计算每对点之间的距离,从而确定出距离最近的点对。例如,在图5-1所示的8个点中,点(1,1)与(2,0.5)是间距最近的点对。

【C++代码】
#include
#include
using namespace std;
class GPoint {
private:
double x, y;
public:
void setX(double x) { this->x = x; }
void setY(double y) { this->y = y; }
double getX() { return this->x; }
double getY() { return this->y; }
};
class ComputeDistance {
public:
double distance(GPoint a,GPoint b) {
return sqrt《a.getX() - b.getX())*(a.getX() - b.getX())
+ (a.getY() - b.getY())*(a.getY() - b.getY()));
}
};
int main()
{
int i,j, numberOfPoints=0;
cout<<"输入点的个数:";
cin>>numberOfPoints;
(1) points= neW GPoint[numberOfPoints];//创建保存点坐标的数组
memset(points,0,sizeof(points));
cout<<"输入"<< numberOfPoints<<"个点的坐标:";
for(i=0;i
double tmpx, tmpy;
cin>>tmpx>>tmpy;
points[i].setX(tmpx);
points[i].setY(tmpy);
}
(2) computeDistance= new ComputeDistance();
int p1=0,p2=1;//p1和p2用于表示距离最近的点对在数组中的下标
double shortestDistance= computeDistance->distance(points[p1], points[p2]);
//计算每一对点之间的距离
for(i=0;i
for(j=i+1;j< (3) ;j++){
double tmpDistance=computeDistance-> (4) ;
if ( (5) ) {
p1=i; p2 =j;
shortestDistance= tmpDistance;
}
}
}
cout<<"距离最近的点对是:(";
cout"points[p1].getX()<<","<
cout<
delete computeDistance;
return 0:
}
-
试题二(共15分)
阅读以下说明和C函数,填充函数中的空缺,将解答填入答题纸的对应栏内。
【说明】
如果矩阵A中的元素A[i,j]满足条件:A[i,j]是第i行中值最小的元素,且又是第j列中值最大的元素,则称之为该矩阵的一个马鞍点。
一个矩阵可能存在多个马鞍点,也可能不存在马鞍点。下面的函数求解并输出一个矩阵中的所有马鞍点,最后返回该矩阵中马鞍点的个数。
【C函数】
Int findSaddle(int a[][N],int M),
{ /*a表示M行N列矩阵,N是宏定义符号常量量*/
int row,column,i,k;
int minElem;
int count=0;/*count用于记录矩阵中马鞍点的个数*/
for( row = 0;row< (1) ;row++) {
/*minElem用于表示第row行的最小元素值,其初值设为该行第0列的元素值*/
(2) ;
for( column = 1;column< (3) ;column++)
if( minElem>a[row][column]) {
minElem = a[row][column];
}
for(k=0;k
if(a[row][k]==minElem){
/术对第row行的每个最小元素,判断其是否为所在列的最大元素*/
for(i=0;i
if( (4) >minElem) break;
if(i>=(5) ){
printf("(%d,%d):%d\n",row,k,minElem);/*输出马鞍点*/
count++;
}/*if*/
}/*if*/
}/*for*/
return count,
}/*findSaddle*/
-
试题一(共15分)
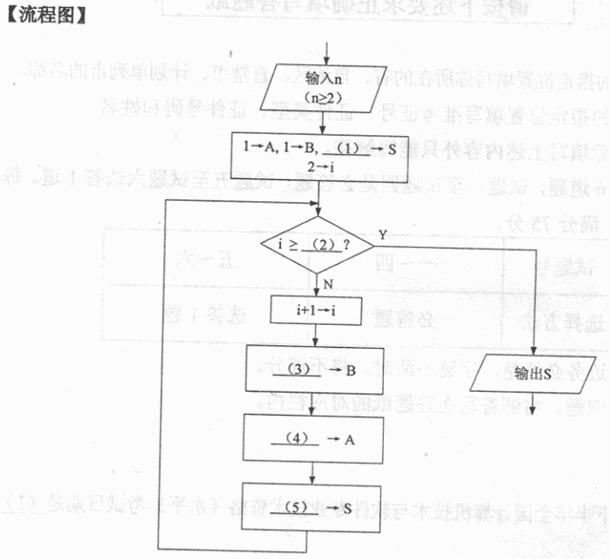
阅读以下说明和流程图,填补流程图中的空缺(1)~(5),将解答填入答题纸的对应栏内。
【说明】
本流程图用于计算菲波那契数列{a1=1,a2=1,an=an-1+ an-2,|n=3,4,…}的前n项(n≥2)之和S。例如,菲波那契数列前6项之和为20。计算过程中,当前项之前的两项分别动态地保存在变量A和B中。