全国2013年4月高等教育自学考试《高等数学基础》试题
-
已知曲线l1:y=lnx及其一条过原点的切线l2,
(1)求曲线l1,切线l2以及x轴围成的平面图形的面积S;
(2)求此平面图形绕x轴旋转所成的旋转体的体积V
-

试求:(1)k的值;(2)方程组的通解.
-
做一个底为正方形,容积为62.5立方米的长方体开口容器,怎样做法用料最省?
-
一平面经过直线(即直线在平面上)l:
 ,且垂直于平面x+y-z+11=0,求该平面的方程.
,且垂直于平面x+y-z+11=0,求该平面的方程. -
求定积分
 .
. -
求不定积分∫arcsinxdx.
-
已知矩阵
 ,求(1-A)-1.
,求(1-A)-1. -
已知y=f(e-x),其中f二次可导,求yn.
-
求极限

-
求函数y=2xcotx+lnx的微分dy.
-
设A是3×4矩阵,其秩为3,若η1,,η2为非齐次线性方程组Ax=b的2个不同的解,则它的通解为
-

-
不定积分

-
曲线y=x2,x=2,y=0所围图形的面积为
-
一动点移动时与A(4,4,0)及坐标平面yoz等距离,则该点的轨迹方程为
-
曲线y=xe-3x的拐点坐标是
-
函数y=ln(1+x2)的单调减少区间是
-
设A,B为n阶可逆阵,则下列等式正确的是
- A.∣A+B∣=∣A∣+∣B∣
- B.AB=BA
- C.∣AB∣=∣BA∣
- D.(A+B)-1=A-1+B-1
-
设空间三点的坐标分别为M(1,1,1),A(2,2,1),B(2,1,2),则∠AMB=
-

- A.12
- B.-12
- C.18
- D.0
-
设f(x)=x3+x=-f(x),则
 的值等于
的值等于- A.0
- B.8
- C.

- D.

-
在区间[-1,1]上满足罗尔定理条件的函数是
- A.f(x)=1-x2
- B.f(x)=∣x∣
- C.f(x)=

- D.f(x)=x2-2x-1
-
下列函数中,求导正确的是
- A.

- B.

- C.

- D.(e-x)′=-e-x
- A.
-
已知∫f(x)dx=xex-ex+c,则∫f′(x)dx=
- A.xex-ex+c
- B.xex-2ex+c
- C.xex+ex+c
- D.xex+c
-
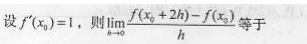
- A.3
- B.2
- C.1
- D.

-

- A.
- B.1
- C.2
- D.-2
-
设矢量
 为非零矢量,且
为非零矢量,且 ,则必有
,则必有- A.

- B.

- C.

- D.
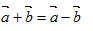
- A.
-
在空间直角坐标系下,方程3x+5y=0的图形表示为
- A.通过z轴的平面
- B.垂直于z轴的直线
- C.垂直于z轴的平面
- D.通过原点的直线
-

- A.0
- B.-1
- C.1
- D.不存在
-
在空间直角坐标系中,点(0,4,-5)在
- A.z轴上
- B.yoz面上
- C.xoz面上
- D.xoy面上

 ,求(1-A)-1.
,求(1-A)-1.


 为非零矢量,且
为非零矢量,且