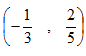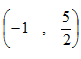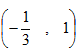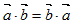全国2015年10月高等教育自学考试《高等数学基础》试题
-
确定a的值,使方程组0
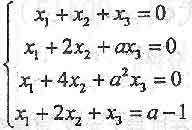 有解,并求其解.
有解,并求其解. -
设曲线y=ax2(a>0,x≥0)与y=1-x2交于点A,过坐标原点0和点A的线与曲线Y=ax2圈成一平面图形,问a为何值时,该图形绕x轴旋转一周所得的旋转体的体积最大?最大体积是多少?
-
用长为18m的钢条围成—个长方体形状的框架,要求长方体的长与宽之比为2:1,问该长方体的长、宽、高各为多少时,其体积最大?最大体积是多少?
-
判断球面x2+y2+z2-12x+4y-6z+24=0与平面2x+2y+z+1=0的位置关系.如果相交,写出它们相交所得圆的一般方程.
-
求定积分
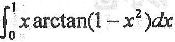 .
. -
求不定积分
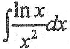 .
. -
求曲线(5y+2)3=(2x+1)5在点(0,-1/5)处的切线方程.
-
已知矩阵a=
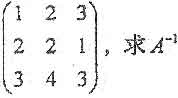 .
. -

-
已知函数y=
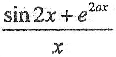 ,求其微分dy。
,求其微分dy。 -
若
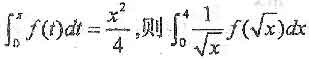 =________.
=________. -
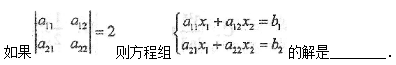
-
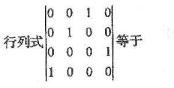
矩阵
 的秩等于________.
的秩等于________. -
不定积分
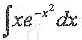 =________.
=________. -
曲线y=(x-5)5/3+2在(+∞,-∞)上有拐点________.
-
平面x—y+2z-6=0与平面2x+y+z-5=0的夹角等于_______.
-
要使函数
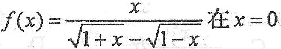 处连续,则应补充定义f(0)= _______.
处连续,则应补充定义f(0)= _______. -
设非零向量
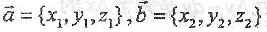 ,则向量
,则向量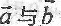 夹角的余弦等于________.
夹角的余弦等于________. -
- A.0
- B.-l
- C.2
- D.1
-
设A为3阶方阵,且∣A∣=-2,则l∣A-1∣等于
- A.-2
- B.-1/2
- C.1/2
- D.2
-
不定积分I=
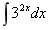 等于
等于- A.
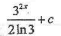
- B.
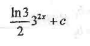
- C.
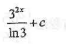
- D.
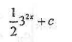
- A.
-
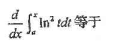
- A.2lnx
- B.ln2t
- C.ln2x
- D.-ln2x
-
下列函数中,在区间[1,e]上满足拉格朗日定理条件的是
- A.1n(1nx)
- B.lnx
- C.1/lnx2
- D.ln (2-x)
-
若f(x)为可微函数,当Δx→0时,在点x处Δy-dy是关于Δx的
- A.高阶无穷小
- B.等价无穷小
- C.低阶无穷小
- D.同阶无穷小
-
若
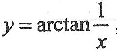 ,则dy等于
,则dy等于- A.
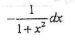
- B.
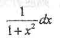
- C.
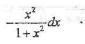
- D.
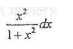
- A.
-
函数
 x的定义域是
x的定义域是- A.
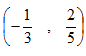
- B.
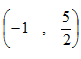
- C.
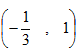
- D.(-1,1)
- A.
-
下列各式中,极限存在的是
- A.
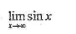
- B.
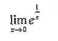
- C.
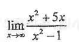
- D.
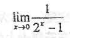
- A.
-
下列关系式错误的是
- A.
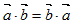
- B.
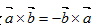
- C.
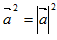
- D.
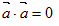
- A.
-
垂直于x轴的平面的一般方程的一般表示式为
- A.Ax+D=0
- B.By+Cz+D=0
- C.Ax+Cz+D=0
- D.Ax+By+D=0
-
点(a,b,c)关于xoz面的对称点坐标为
- A.(-a,-b,-c)
- B.(-a,b,-c)
- C.(-a,b,c)
- D.(a,-b,c)
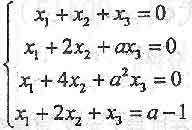 有解,并求其解.
有解,并求其解.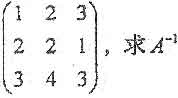 .
.
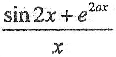 ,求其微分dy。
,求其微分dy。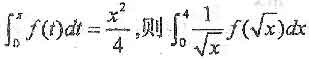 =________.
=________.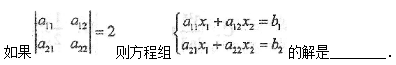
 的秩等于________.
的秩等于________.
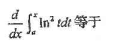
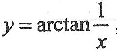 ,则dy等于
,则dy等于