全国2015年4月高等教育自学考试《高等数学基础》试题
-
求抛物线y2=x与直线x-2y-3=0所围的平面图形的面积.
-
当λ为何值时,方程组
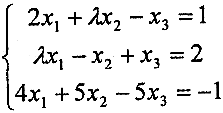 无解、有唯—解或有无穷多组解?在有无穷多组解时,用导出组的基础解系表示全部解.
无解、有唯—解或有无穷多组解?在有无穷多组解时,用导出组的基础解系表示全部解. -
求y轴上一定点(0,b)(b<2)到抛物线x2=4y上的点的最短距离.
-
求定积分
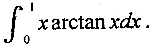
-
求经过点(2,-3,5)且与两平面x一4z=3,2x-y-5z=1的交线垂直的平面方程·
-
设
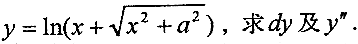
-
计算不定积分
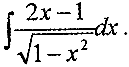
-
设
-
求极限
-
设
-
设A为l0×l5的矩阵,已知它的秩为8,则Ax=0的基础解系所含解的个数为_________·
-
-
设
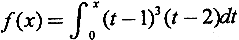 ,则f′(0)= _________·
,则f′(0)= _________· -
曲线
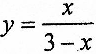 的垂直渐近线是_________·
的垂直渐近线是_________· -
若∫f(x)dx=sin2x+c,则f(x)= _________·
-
空间中一动点移动时与点A(1,2,3)和点B(2,-1,4)的距离相等,则该点的轨迹方程是__________·答案:
-
曲线f(x)=tanx在
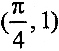 处的切线方程是_________·
处的切线方程是_________· -
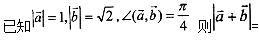
-
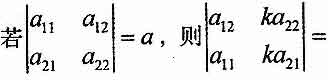
- A.ka
- B.-ka
- C.k2a
- D.-k2a
-
设A,B均为n阶方阵,下面各式正确的是
- A.|A2|=|A|2
- B.A2-B2=(A-B)(A+B)
- C.(A-B)A=A2-AB
- D.(AB)T=ATBT
-
定积分
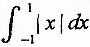 等于
等于- A.0
- B.3
- C.2
- D.1
-
函数f(x)=2x3-6x2-18x+7的极大值是
- A.3
- B.-47
- C.17
- D.-l
-
下列各式正确的是
- A.∫2xdx=2xln2+c
- B.∫sintdt=-cost+c
- C.
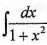 =arctanx
=arctanx - D.
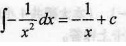
-
设函数f(x)在点a可导,则
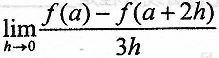 等于
等于- A.
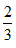 f'(a)
f'(a) - B.
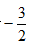 f'(a)
f'(a) - C.
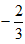 f'(a)
f'(a) - D.
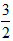 f'(a)
f'(a)
- A.
-
曲线y=2x3-5x2+4x-5在点(2,-1)处切线斜率等于
- A.8
- B.12
- C.-6
- D.6
-
按给定自变量x的变化过程,下列函数为无穷小量的是
- A.

- B.

- C.1-2-x(x→0)
- D.
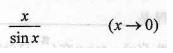
- A.
-
极限
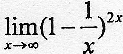 等于
等于- A.
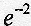
- B.∞
- C.0
- D.
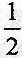
- A.
-
方程2x+3y=1在空间直角坐标系中表示的图形是
- A.平行于xoy面的平面
- B.平行于z轴的平面
- C.经过z轴的平面
- D.直线
-
点M(1,2,-3)关于xoz平面的对称点是
- A.(-l,-2,3)
- B.(-1,-2,-3)
- C.(-l,2,一3)
- D.(1,-2,-3).
-
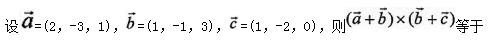
- A.
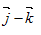
- B.
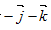
- C.

- D.
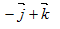
- A.
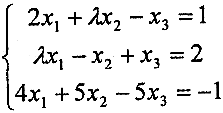 无解、有唯—解或有无穷多组解?在有无穷多组解时,用导出组的基础解系表示全部解.
无解、有唯—解或有无穷多组解?在有无穷多组解时,用导出组的基础解系表示全部解.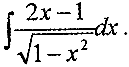
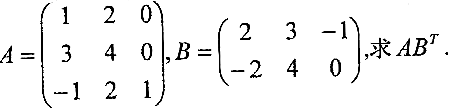
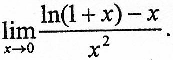
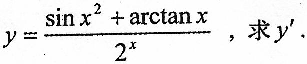
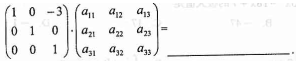
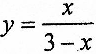 的垂直渐近线是_________·
的垂直渐近线是_________·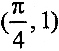 处的切线方程是_________·
处的切线方程是_________·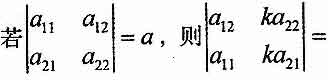
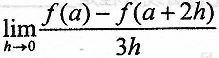 等于
等于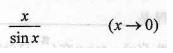
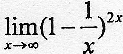 等于
等于