数量方法(二)2016年10月全国统一真题题试卷（00994）

为研究某行业企业年销售额与年销售支出之间的关系，调查获得了5个企业2010年的有关数据如题33表所示：

要求：(1)计算年销售支出与年销售额之间的简单相关系数;(3分)

(2)以年销售支出为自变量，年销售额为因变量，建立线性回归方程;(5分)

(3)估计年销售支出为50万元时企业的预期销售额。(2分)

某疾病的自然痊愈率为20%，为验证某药品的有效性，现从患有该疾病的病人中随机检验抽取了100人，服用该药1个月后40人痊愈。

(1)求服用该药后的病人痊愈率。(2分)

(2)检验该药品是否有效(可靠性取95%)?请给出相应假设检验的原假设和备择假设。 (8分)

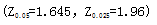
设某种股票2014年各统计时点的收盘价如题30表所示

计算该股票2014年的平均价格。

设有三种股票的价格和发行量资料如题31表所示：

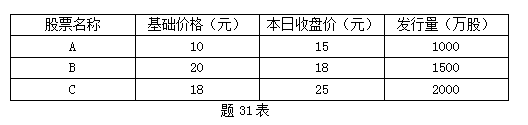
请以发行量为权数计算股票价格指数。

某就业培训中心采用A、B两种培训方法对学员进行某项技能培训。现从经A、B两种 方法培训的学员中分别随机抽取了50人，测得他们掌握该技能的平均时间分别为50 小时和45小时，样本标准差分别为5小时和4小时。求使用A方法和B方法对学员进行技能培训后，掌握该技能的平均时间之差的置信度为95%的置信区间。

已知某螺丝钉生产厂家使用甲、乙、丙三台机床生产的螺丝钉分别占总产量的30%，20%，50%。甲、乙两台机床的废品率分别为3%，5%。从这批螺丝钉中任意抽取一只，已知该螺丝钉为废品的概率是2.9%。求丙机床的废品率。

设X、Y为随机变量，D(X)=6，D(Y)=7，Cov(X，Y)=l，试计算D(2X-3Y)。

某企业20名员工2014年的请假天数如题26表1所示(单位：天)

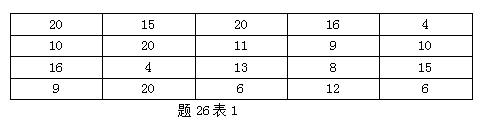
请按照题26表2给出的分组界限进行分组，并按照题26表2给出的格式制作频率分布表。

某企业男性职工占80%，月平均工资为4500元，女性职工占20%，月平均工资为4000元，该企业全部职工的平均工资为_________。

若两个变量的全部观测值都落在一条宜线上，则它们的相关系数为_________。

曼一惠特尼U检验是一种_________统计检验方法，它适用于顺序计量水准的数据。

某种商品的价格今年与去年相比上涨了3%，销售额增长了9%，则商品销售量增长的百分比为

• A.4.5%
• B.5.8%
• C.7.O%
• D.8.O%

一个数据集中出现次数最多的数被称为该数据集的_________。

从总体中随机抽取样本容量为n的样本，用样本均值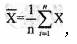，来估计总体均值μ，则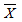是μ的_________估计量。

若销售量增加，销售额持平，则物价指数

• A.降低
• B.增长
• C.不变
• D.趋势无法确定

已知某地区2010年的居民存款余额比2000年增长了1倍，比2005年增长了0.6倍，则2005年的存款余额比2000年增长了

• A.O.25倍
• B.0.5倍
• C.0.75倍
• D.2倍

变量x与y之间负相关是指

• A.x值增大时y值也随之增大
• B.x值减少时y值也随之减小
• C.x值增大时y值随之减小，或X值减小时y值随之增大
• D.y的取值几乎不受x取值的影响

如果变量x与变量y之间没有线性相关关系，以下结论中不正确的是

• A.相关系数r=0
• B.回归系数b=0
• C.r²判定系数=0
• D.估计标准误差Sy=0

对方差已知的正态总体均值的假设检验，可采用的方法为

• A.U检验
• B.t检验
• C.F检验
• D.X²检验

原假设为假时，根据样本推断其为真的概率称为

• A.显著性水平
• B.犯第一类错误的概率
• C.犯第二类错误的概率
• D.错误率

设X1，X2，…，Xn为来自均值为μ方差为σ2的正态总体的简单随机样本，μ和σ2未知，则σ2的无偏估计量为

• A.A
• B.B
• C.C
• D.D

总体真实参数θ的估计值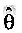与总体真实参数θ之间的离差称为

• A.偏差
• B.方差
• C.标准差
• D.抽样误差

设总体X～N(μ，σ2)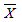，为该总体的样本均值，则

• A.A
• B.B
• C.C
• D.D

对于随机变量X与Y，已知EX=6，EY=2，则E(2X-3Y+5)=

• A.7
• B.9
• C.11
• D.13

在抽样之前将总体划分为互不交叉重叠的若于层，然后从各个层中独立地抽取一定数　　量的单元作样本的抽样组织形式，被称为

• A.纯随机抽样
• B.系统抽样
• C.分层抽样
• D.整群抽样

若随机变量X服从[2，8]上的均匀分布，则EX=

• A.3
• B.5
• C.7
• D.9

标准规定，某零件的内径为10cm，在生产线正常工作情况下，生产出零件的内径误差　　通常服从

• A.二项分布
• B.正态分布
• C.均匀分布
• D.泊松分布

设A、B为两个事件，P(A)=0.7，P(AB)=0.56，则P(B|A)=

• A.O.14
• B.0.26
• C.0.392
• D.0.8

事件A和B相互独立，则

• A.事件A和B互斥
• B.事件A和B互为对立事件
• C.P(AB)=P(A)P(B)
• D.A∩B是空集

某足球运动员罚点球的命中率是90%，则让他罚l0次点球，他罚中的球数是

• A.1
• B.9
• C.10
• D.以上都有可能

对于任意一个数据集来说

• A.一定有众数
• B.可能没有众数
• C.一定有唯一的众数
• D.一定有多个众数

设一个袋子里面有8个编号分别为1～8的球，从中任取一个，观察其编号。用Ω表示样本空间，用A表示事件“抽到奇数号球”，用8表示“抽到偶数号球”，则AB=

• A.{1，3，5，7}
• B.{2，4，6，8}
• C.Ω
• D.空集

以下对极端值最敏感的集中趋势度量是

• A.中位数
• B.众数
• C.标准差
• D.平均数