数量方法(二)2016年4月全国统一真题题试卷(00994)
-
在其它条件不变的情况下,某种商品的供给量(y)与该商品的价格(x)有关。现对给定时期内的价格与供给量进行观察,得到如下一组数据:

现规定选用双曲线函数:
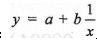 对价格与供给量进行回归分析。
对价格与供给量进行回归分析。要求:(1)以商品的供给量为因变量建立曲线回归方程。
(2)当价格为10元时估计供给量。
-
某管理局所属3个工厂生产同种产品,它们的单位产品成本和产量资料如下:
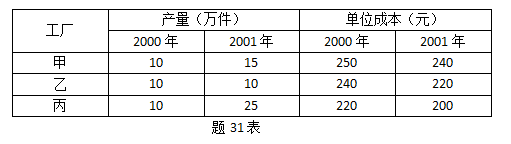
要求:
(1)以2001年产量为权数计算单位成本指数。
(2)以2000年单位成本为权数计算产量指数。
-
在1995年,某地环保组织发现该地区有70%的水域遭到污染。在2005年,环保组织对该地区200个水域组成的随机样本的研究表明,其中有110个水域遭到污染。
(1)求2005年该地区水域遭到污染的样本比率。
(2)2005年该地区水域遭到污染的比率是否比1995年有显著下降(可靠性取95%)?请给出相应假设检验的原假设和备择假设。

-
在一项针对某年龄段的调查中,询问了1000人关于他们获取新闻的主要来源,其中350人表示他们获取新闻的主要来源是互联网。试以95%的可靠性估计该年龄段人口主要通过互联网获取新闻的人数所占比例P的置信区间。
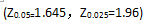
-
某外贸公司1996~2000年驻甲市收购某种土特产品的数量如下表:

要求:
(1)用最小二乘法求出趋势直线方程。
(2)预测2003年收购量。
-
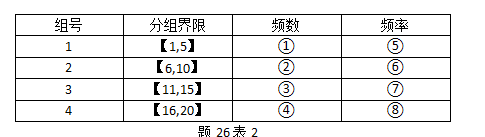
某书店20天的图书销售数据如题26表1所示(单位:册)
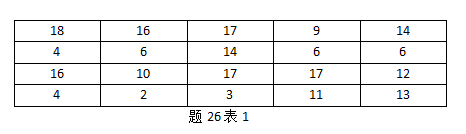
请按照题26表2给出的分组界限进行分组,并按照题26表2给出的格式制作频率分布表, 请将表格中代码①~⑧及所代表的答案内容,答在答题卡上
-
设某工厂的机器一周内发生故障的次数X以及相关的概率为:

求该机器一周平均发生故障的天数。
-
刘某从他家到省科协开会,有三条公交路线,分别是1路、2路和3路公汽。他乘1、2、3路公汽的概率分别为0.4、0.3、0.3,而他乘1、2、3路公汽准时到达的概率分别为0.9、0.6、0.8。如果他准时到达了,则他乘2路公汽去省科协的概率是多少?
-
两个变量之间的简单相关系数r的取值范围为__________。
-
设直线趋势方程为
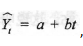 ,若已知
,若已知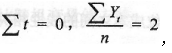 ,则方程中的a等于__________。
,则方程中的a等于__________。 -
利用x2分布对变量的独立性进行检验,己知列联表有3行、4列,检验时x2分布的自由度为__________。
-
在“数量方法”考试中,一个小组5个同学的成绩分别是80、95、84、78、87,则这5个同学的平均成绩是_____________。
-
从抽到的具体样本数据计算出单个估计值作为待估总体参数的估计值的参数估计类型和方法称__________。
-
若企业全员劳动生产率计划规定提高4.5%,实际执行结果提高了6%,则相对全员劳动生产率的计划规定超额完成
- A.-1.57%
- B.1.44%
- C.1.60%
- D.14 .4%
-
综合指数一般是
- A.简单指数
- B.静态指数
- C.加权指数
- D.平均指数
-
定基增长速度与环比增长速度之间的关系是
- A.定基增长速度加l等于各环比增长速度加1后的连乘积
- B.定基增长速度等于各环比增长速度的和
- C.定基增长速度等于各环比增长速度的连乘积
- D.定基增长速度等于各环比增长速度加1后的连乘积
-
设产品产量与产品单位成本之间的线性相关系数为0.86,这说明二者之间存在着
- A.高度相关
- B.中度相关
- C.低度相关
- D.极弱相关
-
若两个变量之间完全相关,在以下结论中不正确的是

- A.A
- B.B
- C.C
- D.D
-
在比较两个非正态总体的均值时,采用Z检验必须满足
- A.两个总体的方差已知
- B.来自两个总体的样本均为大样本
- C.来自两个总体的样本容量相等
- D.两个总体的方差相等
-
在重复抽样时,对于总体比例估计的样本量的确定,以下说法正确的是
- A.样本量将随着允许误差的增加而增加
- B.样本量将随着置信水平提高而增加
- C.样本量随着相对误差的提高而增加
- D.样本量不随置信水平提高而变化
-

- A.A
- B.B
- C.C
- D.D
-
置信系数1--a表示了区间估计的
- A.精确性
- B.不确定性
- C.显著性
- D.可靠性
-
从正态总体N(μ,σ2)中抽取容量为n的样本,由样本均值
 服从的分布是
服从的分布是- A.X2n
- B.t(n)
- C.N(0,1)
- D.F(n,n)
-
在3个相互独立的“是非题”中,每题答对的概率为0.5,则3题中平均答对的题数为
- A.1.0
- B.1.5
- C.2.0
- D.2.5
-
在抽样推断中,样本的容量
- A.越少越好
- B.越多越好
- C.取决于对抽样推断可靠性的要求
- D.取决于统一的抽样比例
-
随机变量的标准差比随机变量的方差
- A.小
- B.大
- C.相等
- D.大小不一定
-
一组数据的每一个观察值与其平均数离差平方的平均数称为该组数据的
- A.标准差
- B.离差
- C.方差
- D.算术平均数
-
事件A、B相互独立,P(A)>0,P(B)>0,则P(A+B)=

- A.A
- B.B
- C.C
- D.D
-
将一枚硬币抛投两次的样本空间Q={00,01,10,11}(用0表示出现正面,用1表示出现反面)。则事件“第一次出现反面”可以表示为
- A.{00,01}
- B.{10,01}
- C.{01,11}
- D.{10,11}
-
某射击运动员的命中率是80%,则让他射击10次,命中的目标数为
- A.1
- B.8
- C.10
- D.以上都有可能
-
某夫妇按照国家规定,可以生两胎。如果他们每胎只生一个孩子。则他们至少有一个女孩的概率为

- A.A
- B.B
- C.C
- D.D
-
已知A省的人均收入是1200元。标准差是100元;B省的人均收入是1300元,标准差是110元,则收入差异较大的省份是
- A.A省
- B.B省
- C.两省相等
- D.不能确定
-
一个由5个工人组成的生产小组负责生产某种零件。今年6月份这5个工人生产的零件分别为53、48、65、50、59,则平均每人生产的零件数是
- A.50
- B.53
- C.55
- D.59






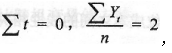 ,则方程中的a等于__________。
,则方程中的a等于__________。

 服从的分布是
服从的分布是
