数量方法(二)2017年10月全国统一真题题试卷（00994）

检查5位同学《数量方法》课的学习时间与学习成绩间的关系，得到如题33表所示的数据

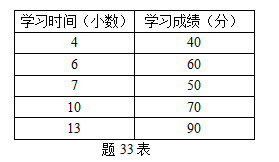
要求：

(1)计算学习时间与学习成绩之间的简单相关系数;

(2)确定学习成绩依赖学习时间的直线回归方程;

(3)计算回归方程的估计标准误差。

对某城市禁止在公共场所吸烟的调查中，接受调查的400名男性中有200人赞同禁止在公共场所吸烟，接受调查的400名女性中有240人赞同禁止在公共场所吸烟。

(1)求男性、女性赞同禁止在公共场所吸烟的比例。

(2)关于禁止在公共场所吸烟，女性赞同的比例是否显著高于男性(可靠性取95%)?给出相应假设检验的原假设和备择假设

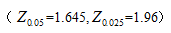
某地2010—2014年某产品产量如题30表所示：

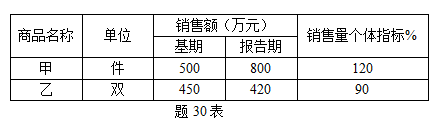
计算：(1)计算销售额总指数;

(2)以基期销售额为权数计算销售量指数。

某市场调查机构对某品牌家电进行市场调查，一共随机调查了1000名顾客，其中有700人表示喜欢该品牌家电。试以95%的可靠性估计喜欢该品牌家电的顾客比例P的置信区间。

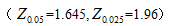
3名射手射击同一目标，各射手的命中率均为0.7，求在一次同时射击中　　(1)目标被击中的概率;　　(2)目标被击中的期望数

某厂生产一批螺丝钉，甲、乙、丙三台机床生产的螺丝钉分别占总量的30%，20%， 50%。这三台机床的废品率分别为3%，5%，2%。求从这批螺丝钉中抽取一只为废品的概率。

一场篮球比赛中，双方20名球员得分情况的分组数据如题26表所示。试计算平均数和方差。分组界限频数

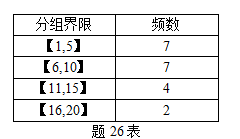
变量之间的关系可分为两种类型，即函数关系和__________。

在趋势分析中，对于趋势线的选择，若数据的二次差大体相同，可配合__________。

在保持样本容量和抽样方式不变的情况下，若要提高置信度则置信区间__________。

对样本数据进行加工并用来判断是否接受原假设的统计量称为__________。

如果两变量无线性相关关系，则其回归方程的回归系数为__________。

称由两个不同时期的总量对比形成的相对数为( )

• A.数量指数
• B.质量指数
• C.零售价格指数
• D.总量指数

某企业今年与去年相比，产量增加了15%，单位产品成本增加了10%，则总生产费用增长( )

• A.4.5%
• B.15%
• C.26.5%
• D.36.5%

已知销售额(Y)对广告费用(X)的回归方程为Y=331.8+3.651X，回归系数3.651的实际意义是( )

• A.广告费用增加一个单位时，销售额平均增加3.651个单位
• B.广告费用为0时，销售额的期望值为3.651个单位
• C.广告费用变动一个单位时，销售额增加3.651个单位
• D.销售额变动一个单位时，广告费用平均增加3.651个单位

根据各季度商品销售额数据计算的各季度指数为：一季度130%，二季度120%，三季度60%，四季度90%。相对来讲受季节因素影响最大的是( )

• A.一季度
• B.二季度
• C.三季度
• D.四季度

设一元线性回归方程为Y=a+bX，若已知b=2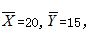，，则a等于( )

• A.-28
• B.-25
• C.25
• D.28

已知变量X与Y负相关，则其回归方程可能是( )

• A.Y=23+15X
• B.Y=4+16X
• C.Y=-56-24X
• D.Y=71+28X

用相关系数来研究两个变量之间线性关系的紧密程度时，应当先进行( )

• A.定性分析
• B.定量分析
• C.回归分析
• D.相关分析

在大样本情况下，对于总体均值的区间估计，若样本容量保持不变，当增大置信水平时，置信区间( )

• A.将变宽
• B.将变窄
• C.保持不变
• D.宽窄无法确定

对正态总体N(μ，6)中的μ进行检验时，采用的统计量是( )

• A.T统计量
• B.Z统计量
• C.F统计量
• D.统计量

从总体N(μ,σ²)中重复抽取容量为n的样本，则样本均值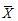的标准差为( )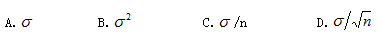

• A.A
• B.B
• C.C
• D.D

样本估计量的数学期望与待估的总体真实参数之间的离差称为( )

• A.均值
• B.方差
• C.标准差
• D.偏差

使用X²分布进行拟合优度检验时，要求每一类的理论频数( )

• A.大于0
• B.不小于5
• C.不小于8
• D.不小于10

随机变量X服从正态分布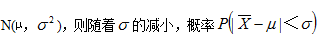将会( )

• A.增加
• B.减少
• C.不变
• D.增减不定

设X与Y为随机变量，D(X)=3, D(Y)=2, Cov(X,Y)=0，则D(5X-3Y)=( )

• A.8
• B.9
• C.87
• D.93

已知P(A)=0.4, P(B|A)=0.7，则P(A-B)=( )

• A.0
• B.0.02
• C.0.12
• D.0.56

袋中有红、黄、蓝球各一个，每一次从袋中任取一球，看过颜色后再放回袋中，共取球三次，颜色全相同的概率为( )

• A.1/9
• B.1/3
• C.5/9
• D.8/9

某种股票的价格周二上涨了10%，周三上涨了4%，两天累计涨幅达( )

• A.4%
• B.5%
• C.14%
• D.14.4%

设随机变量X服从正态分布N(3,16)，则随机变量X的标准差为( )

• A.4
• B.9
• C.12
• D.16

已知甲组工人的平均工资为1000元，标准差为100元。乙组工人的平均工资为800元，标准差为96元。则工资水平差异较大的一组是( )

• A.甲组
• B.乙组
• C.两组相等
• D.不能确定

一般用来描述和表现各成分占全体的百分比的图形是( )

• A.条形图
• B.饼形图
• C.柱形图
• D.线形图