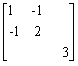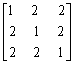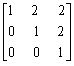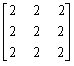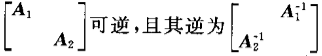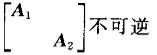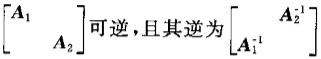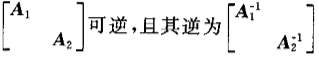线性代数2012年1月真题试题及答案解析(02198)
-
设方阵A满足Ak=O,对某个正整数k成立。证明:A的特征值一定为0。
-
设三阶矩阵A=
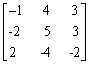 ,求矩阵A的特征值和特征向量。
,求矩阵A的特征值和特征向量。 -
求齐次线性方程组
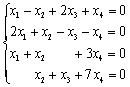 的基础解系和通解。
的基础解系和通解。 -
令f(x1,x2,x3)
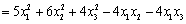 ,写出该二次型对应的矩阵,并判断该二次型是否正定。
,写出该二次型对应的矩阵,并判断该二次型是否正定。 -
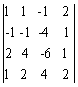
求矩阵A=
 的逆矩阵。
的逆矩阵。 -
设向量组α1=(3,1,2,0), α2=(0,7,1,3), α3=(-1,2,0,1), α4=(6,9,4,3),求其一个极大线性无关组,并将其余向量通过该极大线性无关组表示出来。
-
二次型f(x1,x2,x3)=
 的正惯性指数为_________。
的正惯性指数为_________。 -
计算行列式
 。
。 -
设P为n阶正交矩阵,x是n维单位长的列向量,则 =_________。
-
设α是齐次线性方程组Ax=0的解,而β是非齐次线性方程组Ax=b的解,则A(3α+2β)=_________。
-
设方阵A有一个特征值为-8,则det(8E+A)= _________。
-
实数向量空间V=
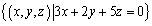 的维数是_________。
的维数是_________。 -
设3阶矩阵A=
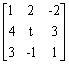 ,B为3阶非零矩阵,且AB=O,则t= _________。
,B为3阶非零矩阵,且AB=O,则t= _________。 -
设α1=(1,0,1),α2=(1,1,1),α3=(0,-1,-1),则-11α1+14α2+9α3=_________。
-
设方阵A满足Ak=E,这里k为正整数,则矩阵A的逆A-1=_________。
-
设方阵A的行列式为5,P为可逆矩阵,则det(P-1AP)=_________。
-
设det(A)=-1,det(B)=2,且A,B为同阶方阵,则det((AB)3)=_________。
-
以下关于正定矩阵叙述正确的是()
- A.正定矩阵的特征值一定大于零
- B.正定矩阵的行列式一定小于零
- C.正定矩阵的乘积一定是正定矩阵
- D.正定矩阵的差一定是正定矩阵
-
设矩阵A=
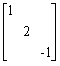 ,则与矩阵A相似的矩阵是()
,则与矩阵A相似的矩阵是()- A.
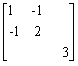
- B.

- C.
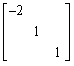
- D.

- A.
-
设三阶方阵A的特征值分别为1/2,1/4,3,则A-1的特征值为()
- A.2,4,1/3
- B.1/2,1/4,1/3
- C.1/2,1/4,3
- D.2,4,3
-
二次型f(x1,x2,x3)=(x1+x2+x3)2的矩阵是()
- A.
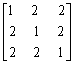
- B.
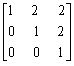
- C.
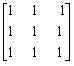
- D.
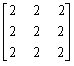
- A.
-
设α1,α2,…,αk是n维列向量,则α1,α2,…αk线性无关的充分必要条件是()
- A.向量组α1,α2,…,αk中任意两个向量线性无关
- B.存在一组不全为0的数l1,l2,…,lk,使得l1α1+l2α2+…+lkαk≠0
- C.向量组α1,α2,…,αk中存在一个向量不能由其余向量线性表示
- D.向量组α1,α2,…,αk中任意一个向量都不能由其余向量线性表示
-
设α=(a1,a2,a3),β=(b1,b2,b3),其中a1,a2,a3不全为0,且b1,b2,b3不全为0,则αTβ的秩为()
- A.0
- B.1
- C.2
- D.3
-
设矩阵A1,A2均为可逆方阵,则以下结论正确的是()
- A.
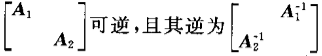
- B.
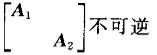
- C.
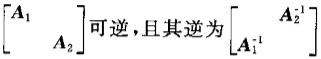
- D.
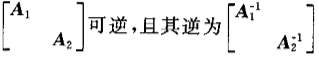
- A.
-
设矩阵A,B,X为同阶方阵,且A,B可逆,若A(X-E)B=B,则矩阵X=()
- A.E+A-1
- B.E+A
- C.E+B-1
- D.E+B
-
设矩阵A是2阶方阵,且det(A)=3,则det(5A)=()
- A.3
- B.15
- C.25
- D.75
-
若矩阵A满足A2-5A=E,则矩阵(A-5E)-1=()
- A.A-5E
- B.A+5E
- C.A
- D.-A
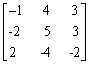 ,求矩阵A的特征值和特征向量。
,求矩阵A的特征值和特征向量。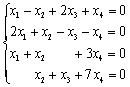 的基础解系和通解。
的基础解系和通解。 的逆矩阵。
的逆矩阵。 。
。 ,B为3阶非零矩阵,且AB=O,则t= _________。
,B为3阶非零矩阵,且AB=O,则t= _________。 ,则与矩阵A相似的矩阵是()
,则与矩阵A相似的矩阵是()