线性代数2013年1月真题试题及答案解析(02198)
-
设A为非零方阵,若存在正整数m,使Am=O,证明A必不能相似于对角矩阵。
-
已知A=
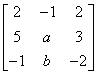 的一个特征向量是=(1,1,-1)T
的一个特征向量是=(1,1,-1)T(1)求a,b;
(2)求A的全部特征值及特征向量。
-
求正交变换X=PY,化二次型f (x1,x2,x3)=-2x1x2+2x1x3+2x2x3为标准形。
-
求向量组
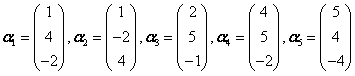 的一个最大无关组,并把其余向量表示为这个最大无关组的线性组合。
的一个最大无关组,并把其余向量表示为这个最大无关组的线性组合。 -
设四元方程组
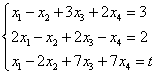 ,问t取何值时该方程组有解?并在有解时求其通解。
,问t取何值时该方程组有解?并在有解时求其通解。 -
二次型f(x1,x2,x3)=(x1-x2+x3)2对应的对称矩阵是_________。
-
设A=
 ,B是三阶方阵,且满足AB-A2=B-E,求B。
,B是三阶方阵,且满足AB-A2=B-E,求B。 -
计算四阶行列式
 。
。 -
若A=
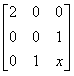 与B=
与B=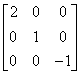 相似,则x=__________。
相似,则x=__________。 -
若三阶矩阵A的特征值分别为1,2,3,则|A+2E|=____________。
-
三元方程组
 的通解是________。
的通解是________。 -
设A=
 ,则A的特征值是____________。
,则A的特征值是____________。 -
设三阶方阵A=[α1, α2, α3],其中αi为A的3维列向量,且|A|=3,若B=[α1,α1+α2,α1+α2+α3],则|B|=_________。
-
设A=
 ,且r (A)=2,则t=_____________。
,且r (A)=2,则t=_____________。 -
设A=
 ,则A-1=________________。
,则A-1=________________。 -
四阶行列式中项a21a32a13a44的符号为_____________。
-
设A、B均为三阶可逆方阵,且|A|=2,则|-2B-1A2B|=__________。
-
对称矩阵A=
 是()
是()- A.负定矩阵
- B.正定矩阵
- C.半正定矩阵
- D.不定矩阵
-
若α=(1,1,t)与β=(1,1,1)正交,则t=()
- A.-2
- B.-1
- C.0
- D.1
-
齐次方程x1+x2-x3=0的基础解系所含向量个数是()
- A.0
- B.1
- C.2
- D.3
-
若3阶方阵A与对角阵
 相似,则下列说法错误的是()
相似,则下列说法错误的是()- A.|A|=0
- B.|A+E|=0
- C.A有三个线性无关特征向量
- D.r(A)=2
-
设向量空间V={ (x1,x2,x3)|x1+x2+x3=0},则V的维数是()
- A.0
- B.1
- C.2
- D.3
-
若同阶方阵A与B等价,则必有()
- A.|A|=|B|
- B.A与B相似
- C.r(A)= r(B)
- D.

-
设α1= (1,0,0)、α2=(2,0,0)、α3=(1,1,0),则()
- A.α1, α2, α3线性无关
- B.α3可由α1, α2线性表示
- C.α1可由α2, α3线性表示
- D.α1, α2, α3的秩等于3
-
设A为三阶方阵,且|A|=2,则|-2A|=()
- A.-16
- B.-4
- C.4
- D.16
-
设A、B为同阶方阵,则必有()
- A.|A+B|=|A|+|B|
- B.AB=BA
- C.(AB)T=ATBT
- D.|AB|=|BA|
-
设n阶方阵A、B、C满足ABC=E,则必有()
- A.ACB=E
- B.CBA=E
- C.BCA=E
- D.BAC=E
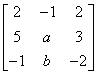 的一个特征向量是=(1,1,-1)T
的一个特征向量是=(1,1,-1)T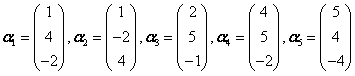 的一个最大无关组,并把其余向量表示为这个最大无关组的线性组合。
的一个最大无关组,并把其余向量表示为这个最大无关组的线性组合。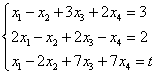 ,问t取何值时该方程组有解?并在有解时求其通解。
,问t取何值时该方程组有解?并在有解时求其通解。 ,B是三阶方阵,且满足AB-A2=B-E,求B。
,B是三阶方阵,且满足AB-A2=B-E,求B。 。
。 与B=
与B= 相似,则x=__________。
相似,则x=__________。 的通解是________。
的通解是________。 ,且r (A)=2,则t=_____________。
,且r (A)=2,则t=_____________。 相似,则下列说法错误的是()
相似,则下列说法错误的是()