线性代数2015年4月真题试题及答案解析(02198)
-
设A,B均为n阶矩阵,且A=B+E,B2=B,证明A可逆。
-
用配方法化二次型f(x1, x2, x3)= x12-2x1x2+x2x3为标准形,并写出所作的可逆线性变换。
-
求矩阵A=
 的全部特征值和特征向量。
的全部特征值和特征向量。 -
问数a为何值时,线性方程组
 有无穷多解?并求出其通解。(要求用它的一个特解和导出组的基础解系表示)
有无穷多解?并求出其通解。(要求用它的一个特解和导出组的基础解系表示) -
求向量组α1=(1,2,1)T,α2=(2,5,1)T,α3=(-1,3,-6)T,α4=(3,-1,10)T的秩和一个极大线性无关组,并将向量组中的其余向量由该极大线性无关组线性表出。
-
设矩阵
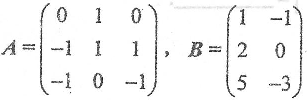 ,矩阵X满足X=AX+B,求X。
,矩阵X满足X=AX+B,求X。 -
设2阶矩阵A的行列式
 ,求行列式|(2A)-1+2A*|的值。
,求行列式|(2A)-1+2A*|的值。 -
二次型f(x1, x2, x3)= x12+2x22+3x32-2x1x2+2x2x3的矩阵为_________。
-
计算行列式D=
 的值。
的值。 -
矩阵
 的两个特征值之和为_______。
的两个特征值之和为_______。 -
若齐次线性方程组
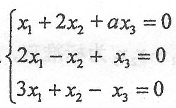 有非零解,则数a=__________。
有非零解,则数a=__________。 -
向量空间
 的维数为_______。
的维数为_______。 -
与向量(1, 0,1)T和(1,1,0)T均正交的一个单位向量为______。
-
若向量组α1=(1,2,1)T,α2=(k-1,4,2)T线性相关,则数k=_______。
-
设矩阵
 ,则ATB-1=_______。
,则ATB-1=_______。 -
设向量α1=(1,-2,2)T,α2=(2,0,-1)T,则内积(α1,α2)=________。
-
设A=
 ,则A*=________。
,则A*=________。 -
设A为3阶矩阵,且|A|=3,则|3A-1|=_________。
-
设3阶实对称矩阵A的全部特征值为-l,1,1,则齐次线性方程组(E-A)x=0的基础解系所含解向量的个数为()
- A.0
- B.1
- C.2
- D.3
-
已知A是2阶可逆矩阵,则下列矩阵中与A等价的是()
- A.
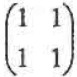
- B.

- C.

- D.

- A.
-
矩阵
 有一个特征值为()
有一个特征值为()- A.-3
- B.-2
- C.1
- D.2
-
若
 ,且2A=B,则()
,且2A=B,则()- A.x=1,y=2
- B.x=2,y=1
- C.x=1,y=1
- D.x=2,y=2
-
设a,b为实数,且
 =0,则()
=0,则()- A.a=0,b=1
- B.a=1,b=0
- C.a=0,b=0
- D.a=1,b=1
 的全部特征值和特征向量。
的全部特征值和特征向量。 有无穷多解?并求出其通解。(要求用它的一个特解和导出组的基础解系表示)
有无穷多解?并求出其通解。(要求用它的一个特解和导出组的基础解系表示)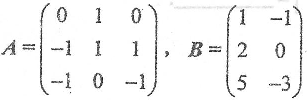 ,矩阵X满足X=AX+B,求X。
,矩阵X满足X=AX+B,求X。 的值。
的值。 的两个特征值之和为_______。
的两个特征值之和为_______。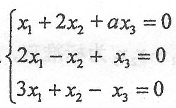 有非零解,则数a=__________。
有非零解,则数a=__________。 ,则ATB-1=_______。
,则ATB-1=_______。 ,则A*=________。
,则A*=________。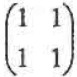



 有一个特征值为()
有一个特征值为() ,且2A=B,则()
,且2A=B,则() =0,则()
=0,则()