线性代数2016年4月真题试题及答案解析(02198)
-
设A为n阶(n≥2)可逆矩阵,证明(AT)*= (A*)T。
-
用正交变换化二次型
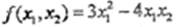 为标准形,并写出所用的正交变换。
为标准形,并写出所用的正交变换。 -
求矩阵
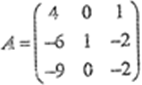 的全部特征值和特征向量。
的全部特征值和特征向量。 -
求线性方程组
 的通解(要求用它的一个特解和导出组的基础解系表示)。
的通解(要求用它的一个特解和导出组的基础解系表示)。 -
求向量组α1=(1,1,2,4)T,α2=(0,1,1,2)T,α3=(2,1,3,6)T,α4=(1,2,3,6)T的一个极大线性无关组,并将向量组中的其余向量由该极大线性无关组线性表出。
-
设矩阵A,B,C满足关系式AC=CB,其中
 ,求A与A3。
,求A与A3。 -
设A为3阶矩阵,将A第1列与第2列互换得到矩阵B,再将B的第2列加到第3 列得到单位矩阵E,求矩阵A。
-
设λ0=-2是n阶矩阵A的一个特征值,则A2+E的一个特征值是_________。
-
若实对称矩阵A与矩阵
 合同,则二次型xTAx的规范形为________。
合同,则二次型xTAx的规范形为________。 -
计算行列式
 。
。 -
设A为3阶矩阵,αi为3维非零向量,且满足Aαi=iαi,则r(A)=_________。
-
设3阶矩阵A的所有元素均为1,则3元齐次线性方程组Ax=0的基础解系中解向量的个数为_________。
-
设向量组α1=(3,1,2)T,α2=(2,1 ,0)T,α3=(1,0, a)T线性无关,则数a的取值应满足________。
-
设矩阵
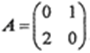 ,则A*=________。
,则A*=________。 -
设矩阵
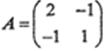 ,则(A-E)-1=_______。
,则(A-E)-1=_______。 -
若行列式
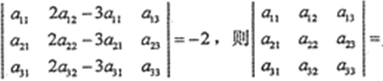 _________。
_________。 -
设矩阵
 ,则ABT=_______。
,则ABT=_______。 -
行列式
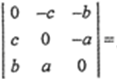 ________。
________。 -
设向量组α1, α2,…, αs(s≥2)线性相关,则α1, α2,…, αs中()
- A.必有一个零向量
- B.必有两个向量对应元素成比例
- C.存在一个向量可由其余向量线性表出
- D.每个向量均可由其余向量线性表出
-
设3阶矩阵A的特征值为-3/2,-2/3,2/3,则下列矩阵中可逆的是()
- A.2E-3A
- B.3E-2A
- C.3E+2A
- D.2E+3A
-
设A为3阶矩阵,且|A|=a≠0,将A按列分块为A=(α1, α2, α3)。若矩阵B =(α1+α2, 2α2, α3),则|B|=()
- A.0
- B.a
- C.2a
- D.3a
-
将3阶矩阵A的第3行乘以-1/2得到单位矩阵E,则|A|=()
- A.-2
- B.-1/2
- C.1/2
- D.2
-
多项式的
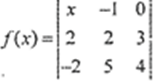 常数项是()
常数项是()- A.-14
- B.-7
- C.7
- D.14
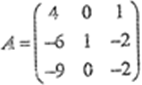 的全部特征值和特征向量。
的全部特征值和特征向量。 的通解(要求用它的一个特解和导出组的基础解系表示)。
的通解(要求用它的一个特解和导出组的基础解系表示)。 ,求A与A3。
,求A与A3。 合同,则二次型xTAx的规范形为________。
合同,则二次型xTAx的规范形为________。 。
。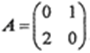 ,则A*=________。
,则A*=________。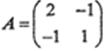 ,则(A-E)-1=_______。
,则(A-E)-1=_______。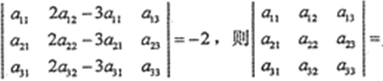 _________。
_________。 ,则ABT=_______。
,则ABT=_______。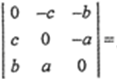 ________。
________。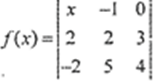 常数项是()
常数项是()