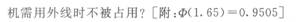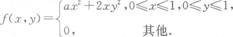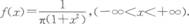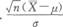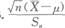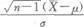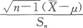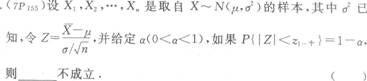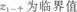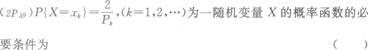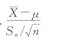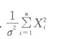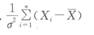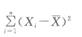2014年4月自学考试《概率论与数理统计(经管类)》专家命题预测试卷(5)
-
某单位内部有l000台电话,每个分机有5%的时间使用外线通话,假定每个分机是否使用外线是相互独立的,该单位总机至少应安装多少条外线,才能以95%以上的概率保证每个分
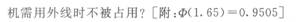
-

求下列随机变量函数的期望:(1)y=2X:
(2)Y=e-2X.
-
设二维随机变量(X,y)的概率密度
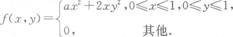
求:(1)常数a;
(2)分布函数F(x,y);
(3)边缘概率密度fx(x),fy(y);
(4)(X,Y)落在区域G={(x,y)|x+y<1|}内的概率.
-
设随机变量X服从柯西分布,其概率密度
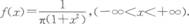
求E(X).
-
设随机变量x服从区间,[0,1]上的均匀分布,y服从参数为1的指数分布,且x与y相互独立,求E(XY).
-

-
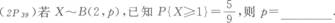
-
(1P11)设A、B为随机事件,已知P(A)=0.7,P(B)=0.5,P(A-B)=0.3,则P(AB)=__________.
-

-
(5P116)设随机变量X的数学期望E(X)=11,方差D(X)=9,则根据切比雪夫不等式估计P{2
-
(4P101)设随机变量X服从参数为3的指数分布,则D(2X+1)=__________
-
有甲、乙两人,每人扔两枚均匀硬币,则两人所扔硬币均未出现正面的概率为___________.
-
甲、乙两人独立地破译一份密码,若他们各人译出的概率均为0.25,则这份密码能破译出的概率为___________.
-
若A1,A2,…,An为样本空间的一个划分,B是任一事件,由全概率公式知,P(B)=___________.
-

-
若随机变量X的分布为

-
已知某产品使用寿命X服从正态分布,要求平均使用寿命不低于1000小时,现从一批这种产品中随机抽出25只,测得平均使用寿命为950小时,样本方差为100小时,则可用检验这批产品是否合格.
-
有n个人,每人都等可能地被分配在N个房间中的任一问(N≥n),则“恰在指定的行间房中各有一人”的概率为___________
-
设随机变量X的分布函数为

-
设随机变量X的数学期望E(X)=75,方差D(X)=5,用切比雪夫不等式估计得P{|X-75|≥k≤0.05,则k=___________.
-
设随机变量X的概率密度为

- A.-3
- B.-1
- C.-1/2
- D.1
-
设随机变量X~N(0,1),y~N(0,1),且X与Y相互独立,则X2+Y2~( )
- A.N(0,2)
- B.x2(2)
- C.t(2)
- D.F(1,1)
-

- A.6
- B.3
- C.1
- D.
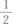
-
(4P96)随机变量X的方差D(X)存在,C为非零常数,则一定有( )
- A.D(X+C)=D(X)+C
- B.D(X-C)=D(X)-C
- C.D(CX)=CD(X)
- D.D(CX+1)=C2D(X)
-

- A.
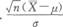
- B.
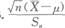
- C.
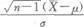
- D.
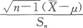
- A.
-
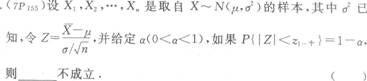
- A.a为置信水平
- B.1-a为置信水平
- C.n为样本容量
- D.
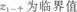
-
设E(X),E(Y),D(X),D(Y)及Cov(X,Y)均存在,则D(X-Y)=( )
- A.D(X)+D(Y)
- B.D(X)-D(Y)
- C.D(X)+D(Y)-2Cov(X,Y)
- D.D(X)-D(Y)+2Cov(X,Y)
-
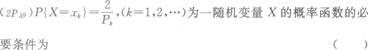
- A.xk非负
- B.xk为整数
- C.O≤Pk≤2
- D.Pk≥2
-

- A.
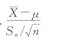
- B.
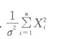
- C.
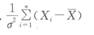
- D.
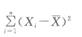
- A.
-
设随机变量X服从参数为2的指数分布,则下列各项中正确的是( )
- A.E(X)=0.5,D(X)=0.25
- B.E(X)=2,D(X)=2
- C.E(X)=0.5,D(X)=0.5
- D.E(X)=2,D(X)=4