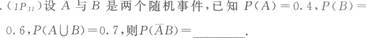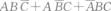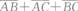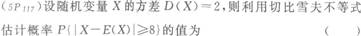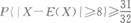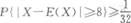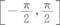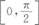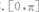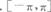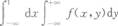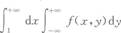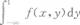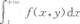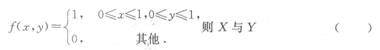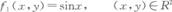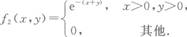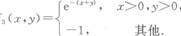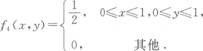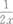2014年4月自学考试《概率论与数理统计(经管类)》全真模拟试卷(4)
-
(4P102)设市场上每年对某厂生产的18寸彩色电视机的需求量是随机变量X(单位:万台),它均匀分布于[10,20].每出售一万台电视机,厂方获得利润50万元,但如果因销售不出而积压在仓库里,则每一万台需支付保养及其他各种损失费用10万元,问18寸彩色电视机的年产量应定为多少台,才能使厂方的收益期望最大?
-

-
设二维随机变量(X,y)的分布律为
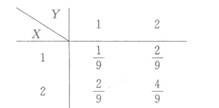
试问:X与y是否相互独立?为什么?
-
设二维随机变量(X,y)的分布律为

(1)求(X,y)分别关于X,Y的边缘分布律;
(2)试问X与y是否相互独立,为什么?
-
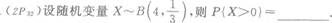
-

-
设事件A与B相互独立,且P(A)=0.3,P(B)=0.4,则P(AUB)=__________.
-

-

-

-
设随机变量x在区间[-1,2]上服从均匀分布,随机变量

-

-
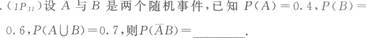
-

-

-
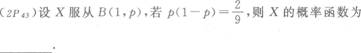
-
设X是连续型随机变量,则P(X=5}=__________.
-

-

-
设A,B,C是三个事件,A,B,C中至少有两个发生的事件是( )
- A.
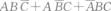
- B.ABC
- C.AB+AC+BC
- D.
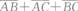
- A.
-
若随机变量X的可能取值为l与口,且P(X=1)=0.4,E(X)=0.2,则a=___________.
-
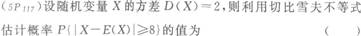
- A.
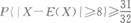
- B.
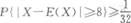
- C.
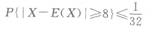
- D.
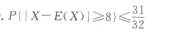
- A.
-

则区间Ⅰ为( )
- A.
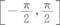
- B.
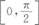
- C.
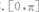
- D.
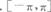
- A.
-
设二维随机变量(x,y)的概率密度为f(x,y),则P{x>1}=( )
- A.
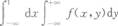
- B.
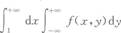
- C.
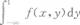
- D.
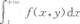
- A.
-
设随机变量X~N(2,4),则D(2X+5)=( )
- A.4
- B.18
- C.16
- D.13
-
设二维随机变量(x,y)的密度函数为
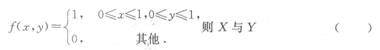
- A.独立且有相同分布
- B.不独立但有相同分布
- C.独立而分布不同
- D.不独立也不同分布
-
(3P66)下列函数中,可以作为某个二维连续型随机变量的密度数的是( )
- A.
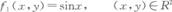
- B.
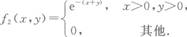
- C.
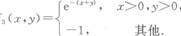
- D.
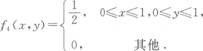
- A.
-
设二维随机变量(X,y)的概率密度为

- A.
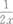
- B.2x
- C.
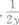
- D.2y
- A.
-
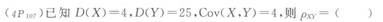
- A.0.004
- B.0.04
- C.0.4
- D.4
-
(2P32)在相同条件下,相互独立地进行5次射击,每次射中的概率为0.6,则击中目标的次数X的概率分布为( )
- A.二项分布B(5,0.6)
- B.泊松分布P(2)
- C.均匀分布UE0.6,33
- D.正态分布N(3,52)