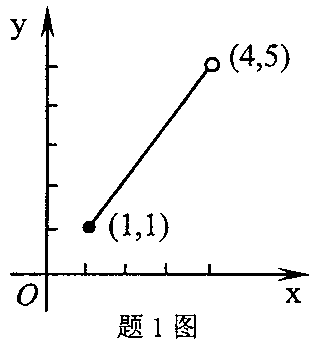全国2012年4月高等教育自学考试《高等数学(一)》试题
-
设函数
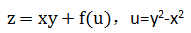，其中f是可微函数. 证明：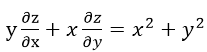
-
设某商品的需求函数为Q(P)=12-0.5P（其中P为价格）.
（1）求需求价格弹性函数.
（2）求最大收益.
-
计算定积分
. -
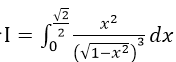设曲线
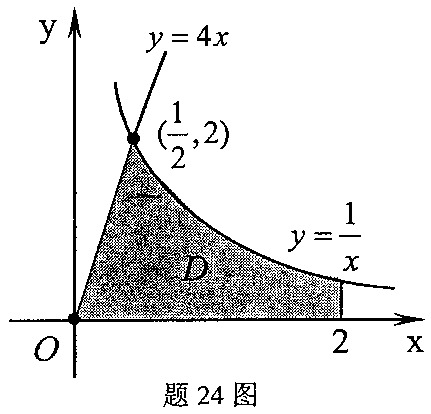
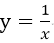与直线y=4x,x=2及x轴围成的区域为D，如图所示. （1）求D的面积A.
（2）求D绕x轴一周的旋转体体积Vx.
-
确定常数a,b的值，使函数
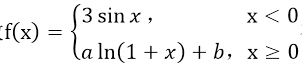在点x=0处可导. -
计算二重积分
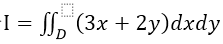，其中D是由直线 x+y=1及两个坐标轴围成的区域，如图所示.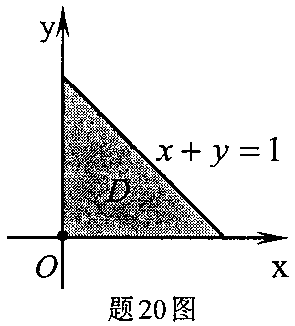
-
计算无穷限反常积分
. -
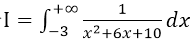求函数
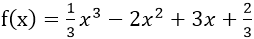的极值. -
设函数
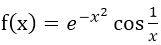，求导数f'(x). -
求极限
. -
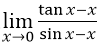设函数
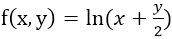，则偏导数
______. -
设
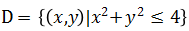，则二重积分
______. -
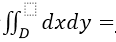微分方程
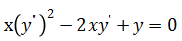的阶数是______. -
导数
______. -
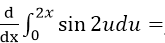函数
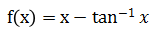在闭区间[-1,1]上的最大值是______. -
设函数f(x)可微，则微分
______. -
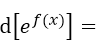曲线y=3x^5-5x^4+4x-1的拐点是______.
-
若级数
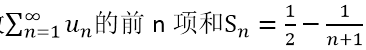,则该级数的和S=______. -
下列积分中可直接用牛顿-莱布尼茨公式计算的是( )
- A.
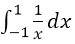
- B.
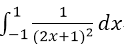
- C.
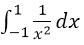
- D.
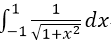
- A.
-
已知
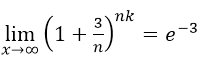，则k=______. -
曲线
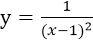的渐近线的条数为 ( )- A.1
- B.2
- C.3
- D.4
-
设函数f(x)可导，且
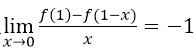，则曲线y=f(x)在点(1,f(1))处的切线斜率为( )- A.1
- B.0
- C.-1
- D.-2
-
当x→0时，下列变量为无穷小量的是( )
- A.
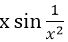
- B.
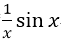
- C.
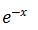
- D.
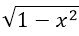
- A.
-
函数y=f(x)的图形如图所示，则它的值域为( )
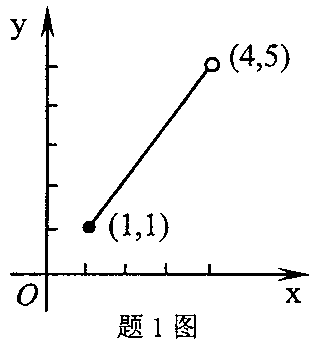
- A.[1,4）
- B.[1,4]
- C.[1,5)
- D.[1,5]
，其中f是可微函数. 证明：
.
与直线y=4x,x=2及x轴围成的区域为D，如图所示. 
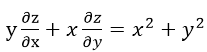
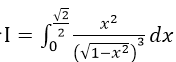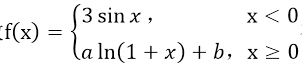在点x=0处可导.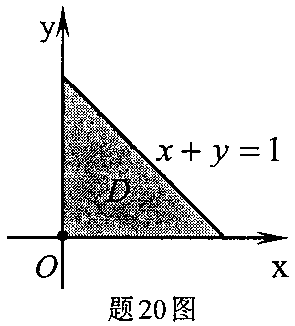
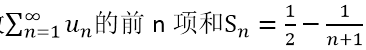，其中D是由直线 x+y=1及两个坐标轴围成的区域，如图所示.
.
的极值.
，求导数f'(x).
.
，则偏导数
______.
，则二重积分
______.
的阶数是______.
______.
在闭区间[-1,1]上的最大值是______.
______.
,则该级数的和S=______.
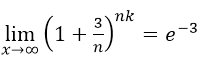，则k=______.
的渐近线的条数为 ( )
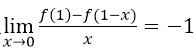，则曲线y=f(x)在点(1,f(1))处的切线斜率为( )
