全国2013年1月高等教育自学考试《高等数学(一)》试题
-
证明当x>0时,
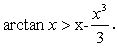
-
设某企业生产一定量的某产品时可用两种原料,第一种为x(千吨),第二种为y(千吨),其电能消耗量N(万度)与两种原料使用量的关系为
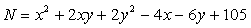
问如何使用两种原料方可使电能消耗达到最低,并求此时的最低能耗.
-
求曲线
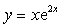 的凹凸区间及拐点.
的凹凸区间及拐点. -
计算定积分
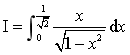 .
. -
设函数
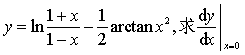 .
. -
计算二重积分
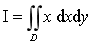 ,其中区域D由曲线
,其中区域D由曲线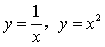 及直线x=2围成.
及直线x=2围成.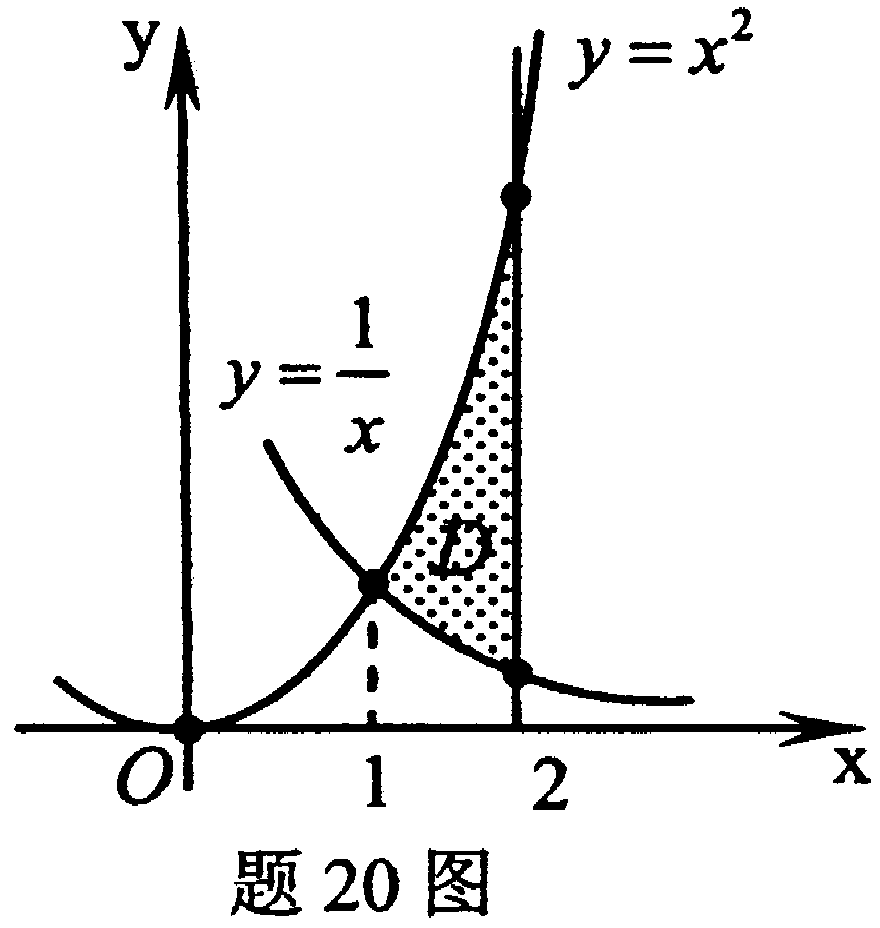
-
求不定积分
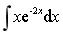 .
. -
设函数
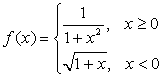 ,计算定积分
,计算定积分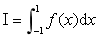 .
. -
设函数
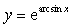 ,求d y.
,求d y. -
设函数z=
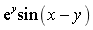 ,则
,则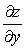 =__________.
=__________. -
讨论函数
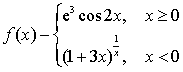 在x=0处的连续性.
在x=0处的连续性. -
微分方程
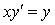 的通解为__________.
的通解为__________. -
若
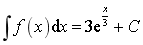 ,则f(x)=__________.
,则f(x)=__________. -
定积分
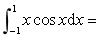 __________.
__________. -
极限
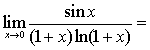 __________.
__________. -
函数
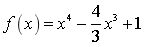 在区间[-1,1]上的最小值为__________.
在区间[-1,1]上的最小值为__________. -
某商品需求量Q与价格P的函数关系为Q=150-2P^2,则P=6时的边际需求为__________.
-
函数
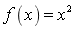 在区间[0,1]上满足拉格朗日中值定理的中值ζ=__________.
在区间[0,1]上满足拉格朗日中值定理的中值ζ=__________. -
设函数
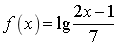 ,则f(x)的定义域为__________.
,则f(x)的定义域为__________. -
极限
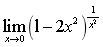 =_________.
=_________. -
曲线
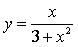
- A.仅有铅直渐近线
- B.仅有水平渐近线
- C.既有水平渐近线又有铅直渐近线
- D.无渐近线
-
若x→0时函数f(x)为x^2的高阶无穷小量,则
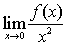 =
=- A.0
- B.1/2
- C.1
- D.∞
-
设函数
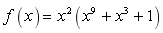 ,则高阶导数
,则高阶导数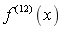 =
=- A.12!
- B.11!
- C.10!
- D.0
-
设函数
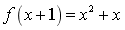 ,则f(x)=
,则f(x)= - A.x(x+1)
- B.x(x-1)
- C.(x+1)(x-2)
- D.(x-1)(x+2)
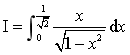 .
.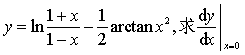 .
.
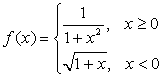 ,计算定积分
,计算定积分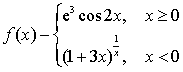 在x=0处的连续性.
在x=0处的连续性.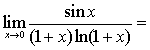 __________.
__________.