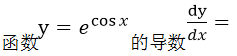全国2017年4月高等教育自学考试《高等数学(一)》试题
-
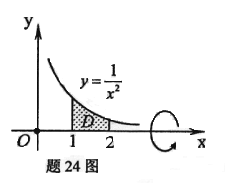
设由曲线
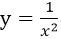 与直线x=1、x=2及x轴所所围成的平面区域为D
与直线x=1、x=2及x轴所所围成的平面区域为D (1)求D的面积A
(2)求D绕x轴一周的旋转体体积为V。
-
计算二重积分
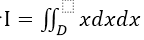 ,其中D是由曲线
,其中D是由曲线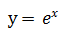 与直线x=1及x轴、y轴所围成的平面区域。
与直线x=1及x轴、y轴所围成的平面区域。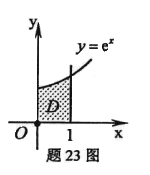
-
计算定积分
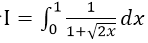
-
设z=z(x,y)是由方程sinz=xyz 所确定的隐函数,求偏导数
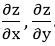
-
设某商品的需求函数为Q(p)=12-p/2,其中p为价格(万元/吨),Q为需求量(吨)
(1)求总收益函数R(p)
(2)问价格为多少时总收益最大?并求最大总收益。
-
求曲线
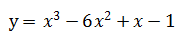 的凹凸区间与拐点
的凹凸区间与拐点 -
求函数
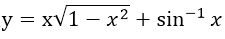 的导数dy/dx
的导数dy/dx -
求微分方程(x+1)dy=(y+2)dx的通解
-
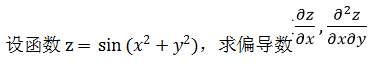
-
求常数a的值,使函数
 在x=0处连续
在x=0处连续 -
求曲线
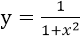 在点(1,1/2)处的切线方程
在点(1,1/2)处的切线方程 -
求极限

-
反常积分
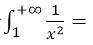
- A.1
- B.2
- C.3
- D.∞
-
判断函数
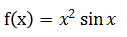 的奇偶性
的奇偶性 -
求极限
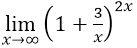
-
已知cos x是f(x)的一个原函数,则不定积分
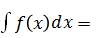
- A.sinx+C
- B.cosx+C
- C.-sinx+C
- D.-cosx+C
-
曲线
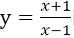 的铅直渐近线为
的铅直渐近线为- A.x=-1
- B.x=1
- C.y=-1
- D.y=1
-
函数
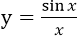 的微分dy=
的微分dy=- A.
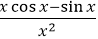
- B.
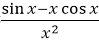
- C.
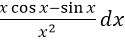
- D.
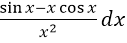
- A.
-
设函数
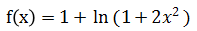 ,则下列结论正确的是
,则下列结论正确的是- A.f(x)只有极小值
- B.f(x)只有极大值
- C.f(x)既有极小值又有极大值
- D.f(x)无极值
-
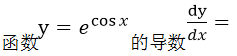
- A.
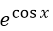
- B.
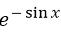
- C.
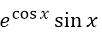
- D.
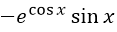
- A.
-
极限
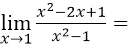
- A.0
- B.1
- C.2
- D.3
-
函数
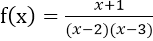 的所有间断点为
的所有间断点为- A.x=-1
- B.x=2
- C.x=3
- D.x=2,x=3
-
下列曲线中经过原点的为
- A.y=x+1
- B.y=x^2-x
- C.y=cosx
- D.x^2+y^2=1
-
设函数f(x)=x^3-x^2-1,则f(1/x)=
- A.1-x+x^2/x^3(分数线左边的为分子)
- B.1+x-x^3/x^3(分数线左边的为分子)
- C.1-x-x^2/x^3(分数线左边的为分子)
- D.1+x+x^3/x^3(分数线左边的为分子)


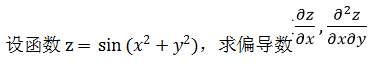
 在x=0处连续
在x=0处连续