高等数学(工本)自考2014年04月真题及答案解析
-
将函数
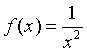 展开为(x-1)的幂级数.
展开为(x-1)的幂级数. -
求曲面
 的面积.
的面积. -
设|x|<1,求幂级数
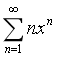 的和函数.
的和函数. -
设函数
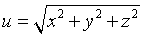 ,证明
,证明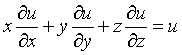 .
. -
求微分方程
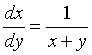 的通解.
的通解. -
判断无穷级数
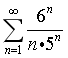 的敛散性.
的敛散性. -
计算对弧长的曲线积分
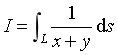 ,其中L为从点A(0,1)到点B(1,0)的直线段.
,其中L为从点A(0,1)到点B(1,0)的直线段. -
验证曲线积分
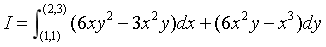 与路径无关,并计算其值.
与路径无关,并计算其值. -
求微分方程xy"+y'=0的通解.
-
计算三重积分
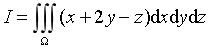 ,其中积分区域Ω:
,其中积分区域Ω: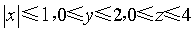 .
. -
计算二重积分
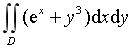 ,其中积分区域是由x=|y|和x=1所围成.
,其中积分区域是由x=|y|和x=1所围成. -
求函数
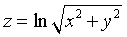 在点(1,1)处的梯度.
在点(1,1)处的梯度. -
设方程
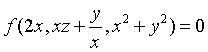 确定函数z=z(x,y),其中f为可微函数,求
确定函数z=z(x,y),其中f为可微函数,求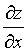 和
和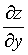 .
. -
求曲面
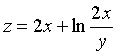 在点(1,2,2)处的法线方程.
在点(1,2,2)处的法线方程. -
设平面π经过点(1,-2,1)和点(7,-5,2),且平行于x轴,求平面π的方程.
-
设函数
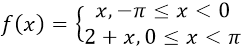 的傅里叶级数的和函数为s(x),则s(0)=_________。
的傅里叶级数的和函数为s(x),则s(0)=_________。 -
设积分区域
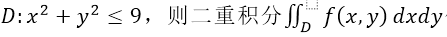 化为极坐标系下的二次积分为 _______。
化为极坐标系下的二次积分为 _______。 -
微分方程
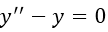 的特征方程为_________。
的特征方程为_________。 -
已知向量a=(3,-1,-2),b=(1,2,-1),则a·b=________。3-2+2=3
-
幂级数
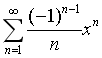 的收敛域是
的收敛域是- A.(-1,1)
- B.[-1,1]
- C.(-1,1]
- D.[-1,1)
-
已知函数
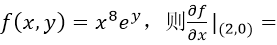 _________。
_________。 -
微分方程
 的满足y(0)=1的特解为
的满足y(0)=1的特解为
- A.
- B.
- C.
- D.
-
在曲线
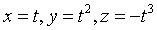 的所有切线中,与平面x+2y+z-3=0平行的切线
的所有切线中,与平面x+2y+z-3=0平行的切线- A.只有一条
- B.只有二条
- C.只有三条
- D.不存在
-
下列曲面方程中,是旋转曲面方程的为

- A.
- B.
- C.
- D.
-
函数f(x,y)=x+y的全微分df(x,y)为
- A.1
- B.2
- C.dx+dy
- D.dx-dy
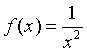 展开为(x-1)的幂级数.
展开为(x-1)的幂级数.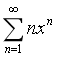 的和函数.
的和函数.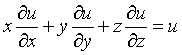 .
.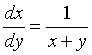 的通解.
的通解.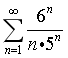 的敛散性.
的敛散性.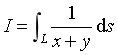 ,其中L为从点A(0,1)到点B(1,0)的直线段.
,其中L为从点A(0,1)到点B(1,0)的直线段.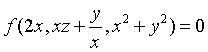 确定函数z=z(x,y),其中f为可微函数,求
确定函数z=z(x,y),其中f为可微函数,求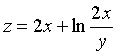 在点(1,2,2)处的法线方程.
在点(1,2,2)处的法线方程.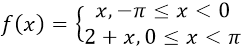 的傅里叶级数的和函数为s(x),则s(0)=_________。
的傅里叶级数的和函数为s(x),则s(0)=_________。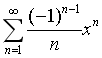 的收敛域是
的收敛域是 的满足y(0)=1的特解为
的满足y(0)=1的特解为
