工程力学(二)2006年4月真题(02391)
-
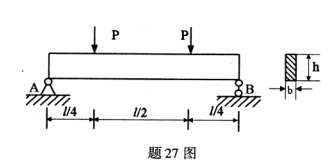
一矩形截面简支梁,梁上荷载如图所示.已知P=6kN、l=4m、b=0.1m、h=0.2m,试画出梁的剪力图和弯矩图并求梁中的最大正应力。
-
正方形截面轴向受压杆如图所示,已知l=1m,a=20mm,材料的弹性模量
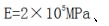 、比例极限σp=200MPa,试判别该杆是否为大柔度杆(细长杆)并求其临界力。
、比例极限σp=200MPa,试判别该杆是否为大柔度杆(细长杆)并求其临界力。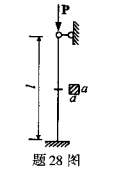
-
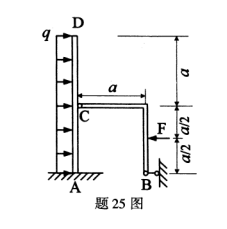
图示结构中,已知均布载荷q和尺寸a,集中力F=qa,求链杆支座B、固定端A处的支座反力。
-
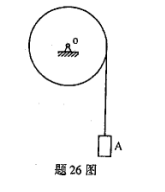
匀质轮
 质量为2m,半径为R,可绕中心轴
质量为2m,半径为R,可绕中心轴 转动.物体A质量为2m,以速度v下降,并通过无重软绳带动轮
转动.物体A质量为2m,以速度v下降,并通过无重软绳带动轮 和质量为m的物体B运动。
和质量为m的物体B运动。(1)求系统动量的投影Py;
(2)对系统应用动量矩定理,求A的加速度aA。
-
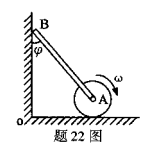
在图示平面机构中,圆盘A的半径为R,沿水平面以角速度ω作纯滚动,AB杆A端铰接在圆盘形心A处,B端沿光滑墙下滑,AB杆长度为l,墙与AB杆的夹角为φ.求平面运动直杆AB的B端的速度。
-
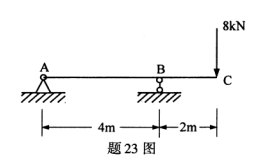
试画出该梁的剪力图和弯矩图。
-
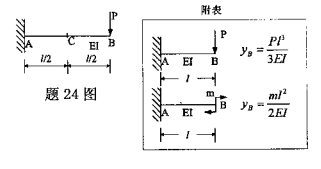
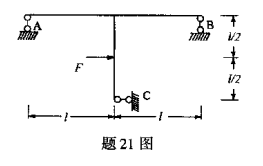
试用叠加法求图示梁C截面的挠度。
-
按图示结构的尺寸和荷载求链杆支座A、B、C的约束反力。
-
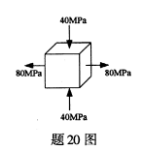
某单元体上的应力情况如图所示,用第三强度理论校核该点的强度时,其相当应力σxd3=( )MPa。
-
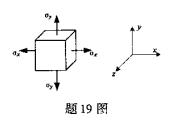
某单元体上的应力情况如图所示,σx、σy,材料的弹性模量E、泊松比μ均为已知,该点沿z方向的线应变εz=( )。
-
图示轴向受拉杆中,P、a、杆的抗拉刚度EA均为已知,该杆的总伸长量△1=( )。

-
胡克定律σ=Eε只在σ≤( )时才成立。
-
脆性材料的抗拉强度
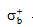 与抗压强度
与抗压强度 之间的关系 为( )。
之间的关系 为( )。 -
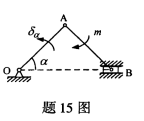
图示曲柄连杆机构中OA=AB=l,当给定曲柄OA的虚位移为δα(方向如图示)时,连杆AB上矩为m的力偶所做的虚功δW=( )。
-
匀质圆轮重为P、半径为R,在质心C上受力W作用而沿地面作纯滚动。给定该惯性力系的主矢
 ,如图所示。根据动静法可求得圆轮与地面间的摩擦力F的值为( )。
,如图所示。根据动静法可求得圆轮与地面间的摩擦力F的值为( )。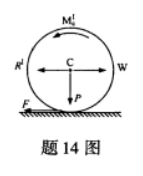
-
刚体定轴转动时,如果非转轴上各点的加速度方向都指向转轴,则该刚体转动的角速度为( )。
-
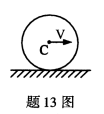
匀质圆轮质量为m、半径为R,在地面上作纯滚动。已知质心C的速度为V,则轮的动能T=( )。
-
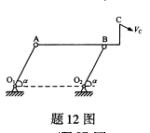
图示机构中O1A=O2B=l,给定折杆ABC上C点的速度Vc,则杆O1A的角速度ω等于( )。
-
材料相同的各圆形截面杆如图所示,当它们受重物Q的自由落体冲击时,抗冲击能力最强者为()
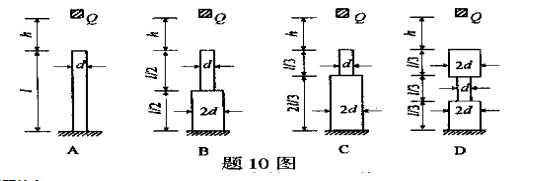
- A.A
- B.B
- C.C
- D.D
-
受横向力作用的工字截面梁如图所示,P的作用线通过截面形心,该梁的变形为()
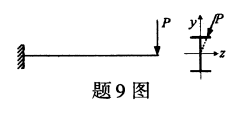
- A.平面弯曲
- B.斜弯曲
- C.平面弯曲与扭转的组合
- D.斜弯曲与扭转的组合
-
图示受扭圆杆中的最大剪应力为()
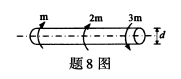
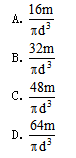
- A.A
- B.B
- C.C
- D.D
-
图示梁为()

- A.静定梁
- B.一次超静定梁
- C.二次超静定梁
- D.三次超静定梁
-
质量为m的质点以初速度V0开始运动(如图示),受重力作用落到水平线ox上.在降落过程中,由质点的受力特征可知()
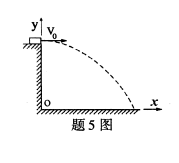
- A.动量的投影Px为常量
- B.动量的投影Py为常量
- C.对O点的动量矩m0(mv)为常量
- D.动能T为常量
-
图示轴向受力杆件中n-n截面上的轴力为()
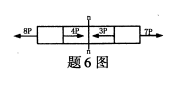
- A.-3P
- B.-4P
- C.+4P
- D.+8P
-
图示机构中,物块A的速度大小为VA,加速度大小为aA,通过绳子带动圆轮绕O轴转动。轮缘上B点的速度及加速度的大小分别为VB、aB,则它们的关系是()
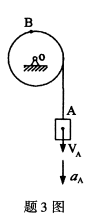
- A.VA=VB,aA=aB
- B.VA=VB,aA>aB
- C.VA>VB,aA=aB
- D.VA=VB,aA
-
图中直杆OA绕O轴转动,带动小环M沿直杆BC运动,若取小环M为动点,取OA为动系,则由牵连运动的定义可知,牵连运动为()
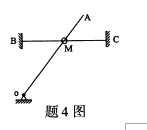
- A.OA杆绕O轴的定轴转动
- B.沿OA杆的直线运动
- C.沿BC杆的直线运动
- D.以OM为半径的圆周运动
-
已知动点弧坐标形式的运动方程为,则t=ls时的速度和切向加速度分别为()
- A.V=l,aτ=0
- B.V=-1,aτ=2
- C.V=-1,aτ=-2
- D.V=l,aτ=2
-
图示不计自重的三铰刚架上作用两个方向相反的力偶m1和m2,且力偶矩的值m1=m2=m(不为零),则支座B的约束反力NB()

- A.等于零
- B.作用线沿A、B连线
- C.作用线沿B、C连线
- D.作用线沿过B的铅垂线