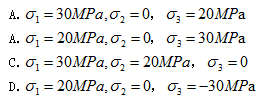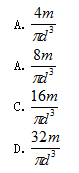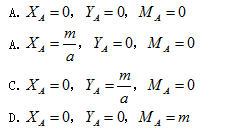工程力学(二)2015年10月真题(02391)
-
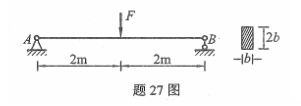
图示矩形截面简支梁AB,已知b=100mm,[σ]=10MPa,不计梁的自重,试求梁能承受的最大荷载Fmax。
-
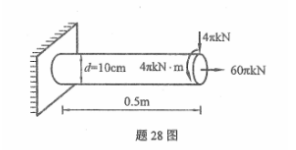
圆截面杆受力及尺寸如图所示,已知[σ]=160MPa,试用第三强度理论校核该杆的强度。
-
图示结构上集中力P=2KN,均布荷载集度q=1KN/m,尺寸a=1m,试求支座A、B的约束反力。
-
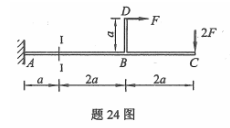
图示悬臂梁受两个外荷载作用,试求悬臂梁1-1截面上的全部内力。
-
图示简支梁的抗弯刚度为EIZ,试用叠加法求该梁A截面的转角。

-
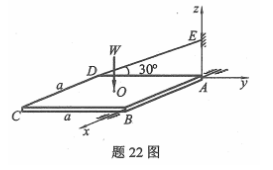
如图所示,匀质方板重W=100KN,边长a=2m,用绳索DE和轴承A、B维持平衡,求绳索DE拉力和轴承B处反力。
-
图示直径为d的钢制圆截面杆受大小未知的外力F作用而发生伸长变形,现测得其上K点处与轴线方向垂直的线应变为ε′,材料的弹性模量为E,泊松比为μ,试求外力F的大小。
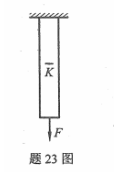
-
压欧拉临界力公式
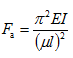 的适用范围为σ≤σp或λ≥( )。
的适用范围为σ≤σp或λ≥( )。 -
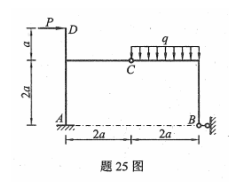
图示钢架结构ABCD上均布荷载集度q=0.5KN/m,水平力F=9KN,尺寸a=2m,求当制作B的约束返利为零时,水平力F的位置x等于多少。
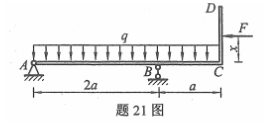
-
图示单元体中的主应力σ1=( )。
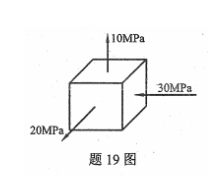
-
图示矩形等截面悬臂梁中的最大切应力τmax=( )。

-
计算梁的弯曲变形时可用叠加法,其适用范围为( )和小变形。
-
平面汇交力系中各力在两个直角坐标轴上投影的( )为零,则该力系一定是平衡力系。
-
受扭圆杆横截面上任一点的切应力大小与该点到横截面圆心的距离成( )。
-
已知图示杆件的总伸长为δ,杆的抗拉刚度为EA,长度为2a,则F=( )。
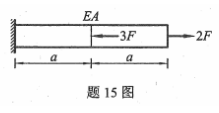
-
图示力F对y轴之矩my(F)=( )。
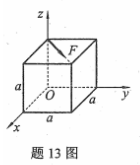
-
如图所示,物块重量W=10KN,力P=1KN,物块与水平接触面之间的静滑动摩擦系数f=0.3,则物块上摩擦力F=( )。

-
当平面任何力系有合力时,合力对其作用面内任何一点之矩,等于各力系中各力对同一点之矩的( )。
-
某点的应力状态如图所示,其主应力为()

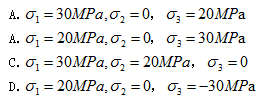
- A.
- B.
- C.
- D.
-
构件的强度时指构件()
- A.抵抗变形的能力
- B.抵抗破坏的能力
- C.保持原有形状下平衡的能力
- D.不产生大变形的能力
-
图示矩形截面对y轴的静矩Sy为()
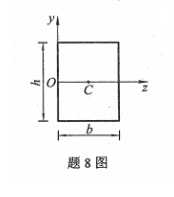

- A.
- B.
- C.
- D.
-
对用积分法计算图示简支梁的位移时,梁的边界条件为()
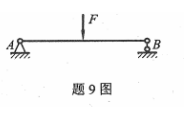

- A.
- B.
- C.
- D.
-
图示长度为l的等截面圆杆,在力偶矩值为m的外力偶作用下的最大切应力为
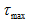 ()
()
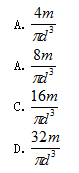
- A.
- B.
- C.
- D.
-
图示结构为()
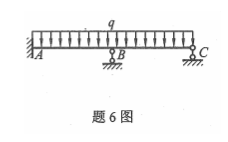
- A.静定结构
- B.一次超静定结构
- C.二次超静定结构
- D.三次超静定结构
-
如图所示,结构上作用两个力偶矩均为m、转向相反的力偶,则A支座的约束反力应为()

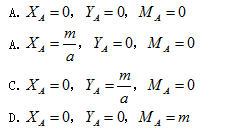
- A.
- B.
- C.
- D.
-
如图所示,平面结构受力F作用,方向如图所示,则支座A处约束反力应为()
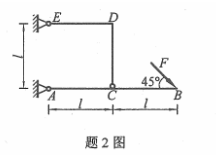
- A.AD方向
- B.AB方向
- C.AE方向
- D.平行于BD连线方向
-
如图所示,已知均质薄板几何形状和尺寸,a=50cm,y轴是薄板对称轴,则其重心的y坐标等于()
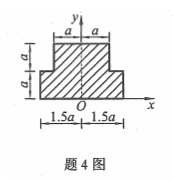

- A.
- B.
- C.
- D.
-
如图所示,平面汇交力系由F1、F2、F3三个力组成,其中F1=50KN,F2=200KN,且各力在y轴的投影之和∑y=0,则力F3应等于()

- A.150KN
- B.100KN
- C.75KN
- D.50KN







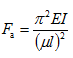 的适用范围为σ≤σp或λ≥( )。
的适用范围为σ≤σp或λ≥( )。