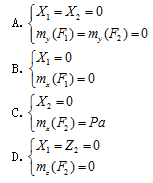工程力学（二）2014年4月真题（02391）

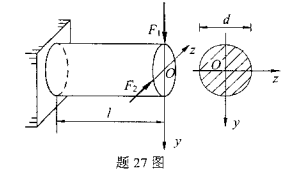
圆形截面悬臂梁如图所示，已知F1=lkN，F₂=2kN，l=2m，d=100mm.试求梁的最大拉应力。

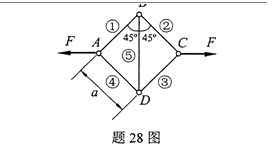
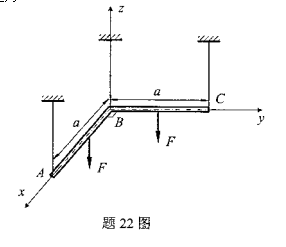
图示正方形桁架，各杆的抗弯刚度EI、横截面积S均相同，且均为细长杆，其中①、②、③、④杆长度为a.若桁架在面内失稳，求桁架达到临界状态时的力F。

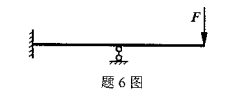
试画出图示简支梁的剪力图和弯矩图.已知q，

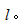
平面结构尺寸、约束及荷载如图所示，试求绳索CD的拉力和固定端支座A处的约束反力。

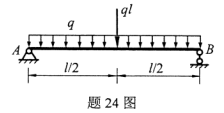
图示简支梁AB，在B支座处受集中力偶m作用，试用积分法分别求A、B两截面的转角。

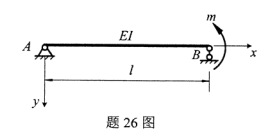
匀质直角折杆如图所示，两段重量均为F=2kN，长度为a=2m，在三根铅垂绳索支撑下保持平衡，求各绳索的拉力。

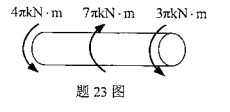
受扭圆形截面杆如图所示，已知杆的直径d=100mm，材料的许用切应力[τ]=70MPa.试校核杆的强度(π取3.14)。

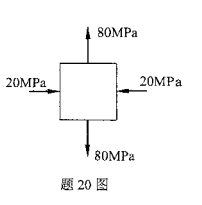
某危险点处应力状态如图所示，则第三强度理论的相当应力σ_r3=( )。

平面应力状态的广义胡克定律中，εx=( )。

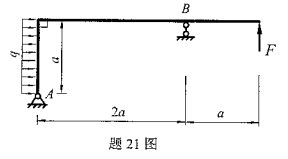
如图所示，已知集中力F与均布荷载集度q=2F/a，求A、B支座反力。

受横力弯曲的矩形截面梁，上、下边缘处的切应力为( )。

在推导梁的弯曲正应力公式时，需要综合考虑几何方面、静力学方面和( )的关系。

图示截面为正方形的木榫接头剪切面的面积为( )。

物体的重心就是物体重力合力的作用点，只有( )物体的重心与形心重合。

静滑动摩擦系数f是( )的大小与法向反力大小的比例系数。

合力对任一轴的投影，等于其各分力对同一轴投影的( )。

力偶使物体转动的效果只由力偶矩确定，与( )的位置无关。

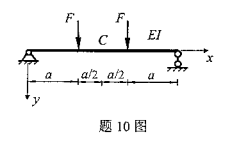
图示梁中点C处的转角为()

• A.
• B.
• C.
• D.

作用在刚体上的两个力大小相等、方向相反，则这两个力平衡的条件是( )。

图示圆形截面对z轴的静矩Sz为()

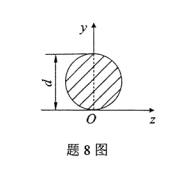
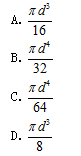
• A.
• B.
• C.
• D.

图示纯弯曲梁横截面上A点处的正应力为4MPa，z为中性轴，B点处的正应力为()

• A.2MPa
• B.4MPa
• C.6MPa
• D.8MPa

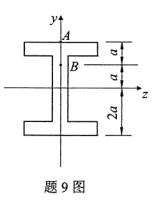
图示结构为()

• A.静定结构
• B.一次超静定结构
• C.二次超静定结构
• D.三次超静定结构

材料的许用应力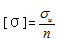(n为安全系数)，对于脆性材料，极限应力σ_U取材料的()

• A.比例极限
• B.弹性极限
• C.屈服极限
• D.强度极限

图示平面汇交力系汇交于A点，各力大小和方向如图所示，则该力系合力R的大小为()

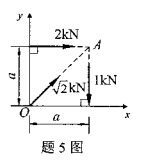
• A.R=0
• B.R=1kN
• C.R=2kN
• D.R=3kN

图示空间力系，F₁=F₂=P，则下面正确的计算结果是()

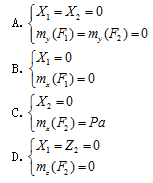
• A.
• B.
• C.
• D.

如图所示，物块与铅垂墙面之间的静摩擦系数为f=0.3，水平主动力F的大小与物块重量W相等，F=W则使物块平衡的最小拉力T值为()

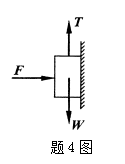
• A.0
• B.0.3W
• C.0.7W
• D.W

在图示平面力系中,其作用点分别为C、O、B点，距离OB=20cm，则此力系向O点简化的结果为()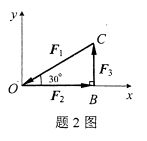

• A.R′=0，M_O=0
• B.R′=0，M_O=20kN·cm
• C.R′=0，M_O=40kN·cm
• D.R′=2kN，M_O=20kN·cm

如图所示的简支梁，其正确的受力图为()

• A.
• B.
• C.
• D.