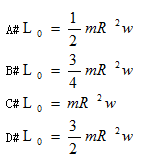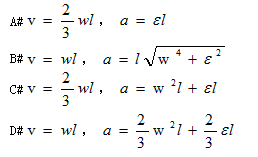工程力学(二)2004年4月真题(02391)
-
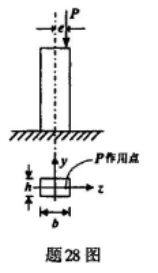
矩形截面偏心受压杆如图所示,P的作用点位于柱顶端截面的z轴上,P、b、h均为已知。试求杆的横截面上不出现拉应力时的最大偏心距。
-
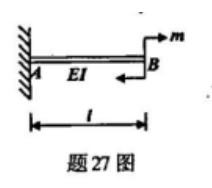
试用积分法求图示梁中B截面的转角和挠度。
-
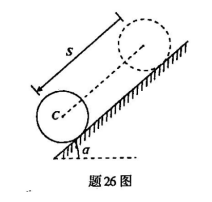
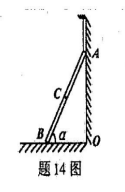
匀质圆轮C质量为m,半径为R,受重力作用沿与水平面夹角为a的斜面无初速度地滚下(无滑动),如图中所示以S表示轮心c沿斜面走过的路程。试用动能定理求图示位置轮心c的速度和加速度。
-
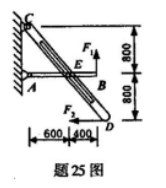
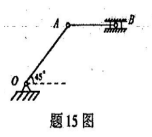
如图所示机构由AB、CD两杆组成,固结在AB杆上的销钉E可沿着CD杆中间的光滑直槽滑动,结构在图示位置平衡,这时AB杆处于水平位置,CE=ED、AE=600mm、EB=400mm,图中尺寸单位为mm。若已知F1=3KN,求铰支座A处的约束反力及力F2的值。
-
摆轴向受压圆形截面杆如图所示,已知ι=2m、d=4cm、材料的弹性模量
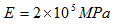 、比例极限
、比例极限 ,试验算该杆可否用欧拉公式
,试验算该杆可否用欧拉公式 计算其临界力。
计算其临界力。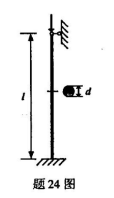
-
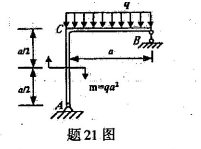
求图示结构A和B处的支座反力。
-
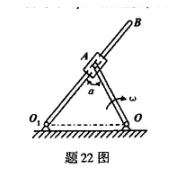
摆杆机构如图,曲杆OA长R,且以角速度 MPa绕O轴转动,并通过套在摆杆O1B上的滑块A带动O1B摆动,设图示位置下∠O1AO=a,O1A=AB=2R。用速度合成定理求该瞬时杆O1B的角速度,并求B点的速度。
-
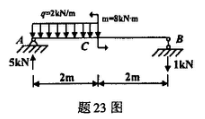
摆图示梁的支座反力值已算出并标示在图中,试画出该梁的剪力图和弯矩图。
-
横杆件受自由落体冲击时的动荷系数Kd=( )。
-
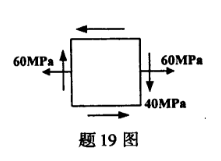
某单元体上的应力情况如图所示,该点处的最大主应力
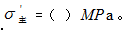 =( )。
=( )。
-
直径为d的圆形截面直杆,其抗扭截面模量Wp=( )。
-
横截面积为A的登直杆,受轴向拉力P,最大剪应力
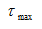 =( )。
=( )。 -
横截面积和长度相同的两简支梁,一为正方形截面,另一为圆形截面,两梁上承受相同的横向荷载(作用在通过弯曲中心的纵向平面内)产生弯曲时,从梁的强度方面考虑,( )截面更合理。
-
图示匀质杆AB长为ι,质量为m,A端用绳挂住,处于静止状态。设将绳剪断瞬时杆的角加速度为ε,则该瞬时杆的惯性力系的主矩值为
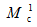 =( )。
=( )。
-
图示体系中杆AB长为ι,杆OA长为
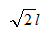 。当给杆OA一虚位移δφ时,B点的虚位移值
。当给杆OA一虚位移δφ时,B点的虚位移值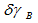 =( )。
=( )。
-
图示系统中物A的质量为m1,匀质纯滚动轮C质量为m2,不记软绳质量。当物体A以速度
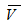 运动时,该系统的动量在X轴的投影为Kx=( )。
运动时,该系统的动量在X轴的投影为Kx=( )。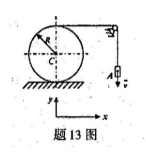
-
火车轮尺寸如下图,沿铁轨无滑动滚动,已知轮心O的速度V0,则由瞬心法可知A点的速度VA=( )。
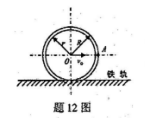
-
某点的应力状态如图所示,用第三强度理论校核该点强度时,其相当应力
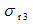 为()
为()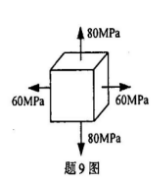

- A.A
- B.B
- C.C
- D.D
-
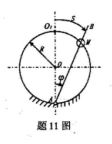
杆AB绕A点转动带动套环M在固定圆环上运动。已知固定圆环半径R,AB杆转动方程为φ=wt,用图中给定的远点按自然法表示的M点的运动方程是S=( )。
-
压杆的柔度值决定于()
- A.压杆的长度
- B.压杆的长度和截面尺寸
- C.压杆的长度和杆两端的约束情况
- D.压杆的长度、截面的形状和尺寸以及杆两端的约束情况
-
长度和横截面面积均相同的两直杆,一为钢杆,另一为铝杆,在相同的拉力作用下()
- A.铝杆的应力和钢杆相同,而变形大于钢杆
- B.铝杆的应力和钢杆相同,而变形小于钢杆
- C.铝杆的应力和变形都大于钢杆
- D.铝杆的应力和变形都小于钢杆
-
长圆杆ABCD受力如图所示,其BC段的扭矩
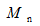 是()
是()
- A.m
- B.-m
- C.-2m
- D.-3m
-
对塑性材料来说,
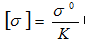 中的极限应力σ0为材料的()
中的极限应力σ0为材料的()- A.比例极限
- B.弹性极限
- C.屈服极限
- D.强度极限
-
匀质圆盘质量为m,半径为R,绕通过盘缘上O点的轴以角速度转动。该圆盘相对O轴动量矩的值为()

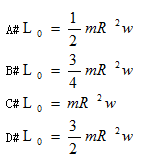
- A.A
- B.B
- C.C
- D.D
-
如图所示
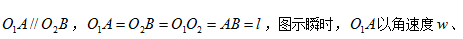 角加速度绕转动,则T形杆上D点的速度v和加速度a的大小分别是()
角加速度绕转动,则T形杆上D点的速度v和加速度a的大小分别是()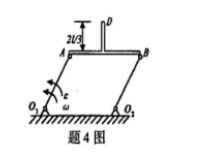
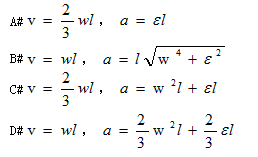
- A.A
- B.B
- C.C
- D.D
-
图示机构中,OE以匀角速度绕O转动,已知OE=
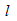 ,通过连杆EF带动滑块F在水平槽中滑动,在图示位置∠OEF=90°,∠OFE=30°,则该瞬时滑块的速度VF等于()
,通过连杆EF带动滑块F在水平槽中滑动,在图示位置∠OEF=90°,∠OFE=30°,则该瞬时滑块的速度VF等于()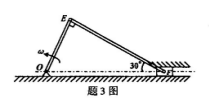

- A.A
- B.B
- C.C
- D.D
-
一动点的运动方程是x=sint,y=2cos2t,则t=0时的动点的速度和加速度是()
- A.v=0,a=0
- B.v=0,a=8
- C.v=1,a=-8
- D.v=1,a=0
-
在边长为a的正方体的顶面内沿对角线DB作用一大小为F的已知力,则该力在x轴的投影Fx及对x轴之矩mx(F)分别是()
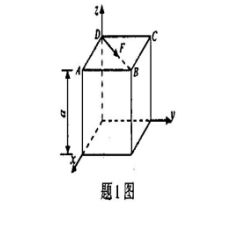

- A.A
- B.B
- C.C,mx(F)=0
- D.D,mx(F)=




 计算其临界力。
计算其临界力。