离散数学2016年4月考试真题(02324)

符号化下列命题，并构造推理证明。

中华牙防组委员会成员都是教授，并且是牙医;有些中华牙防组委员会成员是资深专家。所以，有的中华牙防组委员会成员是牙医，且是资深专家。

用Kruskal算法求题35图中的一棵最小生成树，并画出此树。(须写出详细过程)

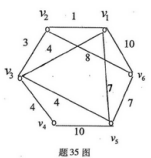
设A，B，C是集合。证明 A ∩(B ∪ C)= (A ∩ B)∪(A ∩ C)

设G是无向简单图，有2n个结点且每个结点度数均为a。证明：G是连通图。

设是独异点，是单位元，且S中任意x有x?x = e。证明：是交换群。

设解释 I如下：D ={2,3}，已知f(2) =3，f(3) =2，F(2) =0，F(3)=1，G(2,2) =G(2,3)=0，G(3,2)= G(3,3) =1。

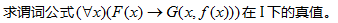
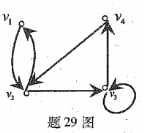
设图G如题29图所示。

(1)写出图G的邻接矩阵;

(2)G中长为4的通路有几条?

(3)其中有几条回路?

设S(x)：x 是人，G (x)：x会思考，则命题“人都会思考”可符号化为________。

—个具有10个顶点的简单连通无向图的边数至少为________，至多为________。

设集合A有3个元素，则A上的等价关系有________个。

设A ={2，4，6，12}，a*b= gcd(a，b)，即a、b的最大公约数。代数系统，* >的幺元是 ________，零元是 ________。

设{<3,1 >,<2,3 >,<5,3 >,<3,4 >} 是集合A = {1，2，3，4，5}上的关系，则domR=________，ranR=________。

若连通平面图G有10条边，4个面，则G有________ 个顶点。

设A={1，2，3，4}，B = {1，2，4，5}， A到S的关系R = {<2,4>,< 1,1 >,<4,2>}， B到A的关系 S = {< 4,1 >,< 1,4 >,< 2,3 >}。则S。R=_______。

设集合A ={1，3，4}以及A上的一个二元关系R = {<1,3>,<3,4>,<3,3>}，则自反闭包r(R)=_________，R^-1=_________

设A= {3，2，4}，B = {2，5，3}，则A十B =________，A-B=________。

设简单无向图G有16条边，有3个4度结点，有4个3度结点，其余结点的度数均大于3，则G中的结点个数至多为()

• A.9
• B.10
• C.11
• D.12

设S = {1，{1}，{1,2}}，则既是S的元素又是S的子集的为()

• A.
• B.1
• C.{1}
• D.{1,2}

设论域为整数集，下列公式中真值为假的是()

• A.
• B.
• C.
• D.

下列图对应的格是有补格的是()

• A.
• B.
• C.
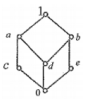
• D.

在整数集Z上，下列运算满足结合律的是()

• A.a*b=|a-b|
• B.a*b=ab+1
• C.a*b=2a+b
• D.a*b=a+b+1

• A.约束变元
• B.既是自由变元，也是约束变元
• C.自由变元
• D.既不是自由变元，也不是约束变元

设p：他怕困难，q：他获得成功。命题“他只有不怕困难，才能获得成功”可符号化为()

• A.p→q
• B.q→p
• C.┐p→q
• D.q→┐p

5个结点的非同构的无向树的数目是()

• A.5
• B.4
• C.3
• D.2

设A ={1，2，3，4，5，6}，≤为A上的整除关系，则A的最小元为()

• A.1
• B.3
• C.4
• D.6

—颗树有2个3度结点，其余结点都是叶子，则叶子数是 ()

• A.7
• B.6
• C.5
• D.4

下列集合关于数的加法和乘法运算不能构成环的是()

• A.自然数集合
• B.整数集合
• C.有理数集合
• D.实数集合

设R（x）：是实数，L（x，y）：x

• A.
• B.
• C.
• D.

偏序关系一定不是()

• A.自反的
• B.传递的
• C.反自反的
• D.反对称的

下列语句为复合命题的是()

• A.今天天气凉爽
• B.今天天气炎热，有雷阵雨
• C.x+y>16
• D.今天天气多好呀，外面景色多美呀

下列命题公式为永假式的是()

• A.
• B.
• C.
• D.