自考计算机网络数据结构模拟试卷七

阅读下列算法,并回答问题:

(1)假设数组L[8]={3,0,5,1,6,4,2,7},写出执行函数调用f33(L,8)后的L

(2)写出上述函数调用过程中进行元素交换操作的总次数。

void f33(int R[],int n)

{int i,t,

for(i=0;

while(R[i]!=i)

{t=R[i][j]:

R[R[i]]-R[i]

R[i]=t;

}

(1)

(2)

已知二叉树的定义如下:

typedef struct node{

int data;

struct node *Ichild, rchild;

}* Bitptr;

编写递归算法求二叉树的高度。函数原型为:intf34(Bitptr)

下面的算法是将给定的关键字序列依次插入散列表中,请仔细阅读程序并把未完成的部分填上。

void HashInsert( HashTable T, NodeType new)

{ }//将新结点new插入散列表T[om-1]中

int (  (1)  ),sign;

sign=HashSearch(t,new.key,&pos);//在表T中查找new的插入位置

if(  (24)  )//找到一个开放的地址pos

t[pos]=  (3)  )//插入新结点new,插入成功

else  //插入失败

f(  (4)  )

printf("duplicate key!");//重复的关键字

else

//sign

Error("hash table overflow!");//满错误,终止程序执行

//HashInsert

（1）

（2）

（3）

（4）

下面的算法在中序线索树中找由指针p所指结点的后继并由指针指向该后继结点,试补充完整(线索树的结点有五个域data, Ichild, rchild,左、右标志域ltag、rtag,并规定标志0指向孩子,1指向线索 Bin ThrNode为结点类型)

BinThrNode inorder_ next(BinThrNode *p)

{

BinThrNode*q

(1)   ;

if (p->rtag-0)

while((2))q=(3)

return(q);

}

(1)

(2

(3)

简述队列的概念及其特点。

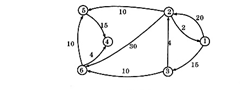
对题图所示的有向图,试利用 Dijkstra算法求出从源点1到其他各顶点的最短路径,并写出算法的动态执行情况。

?下面的排序算法的思想是:第一趟比较将最小的元素放在r[1]中,最大的元素放在r[n中,第二趟比较将次小的放在r[2]中,将次大的放在r[n-1中依次下去,直到待排序列为递增序列。(注:代表两个变量的数据交换)

void sort(intr[],intn)

{

int i=1,j,t,min, max;

while(i

{

min=max=i:

for (j=i+;j<=n-i+1:++j)

{

Ifr[j]

else if(r[j]>r[max])(2) ;

r[min] r[i];

(3) 

i++

}

}

(1)

(2)

(3)

求下列广义表的长度length()和深度 depth)

(1)a=((a),((b),c),d)

(2)B-(a,(a,b),d,e,((i,),k)

设二维数组Ax的每个元素占4个字节已知LOC(a)=100,A共占多少个字节?A的终端结点a45的起始地位为何?按行和按列优先存储时,a2的起始地址分别为何?

已知广义表LS=((a,x,y,z),(b,c)),运用head和tail函数取出原子c的运算是( )

数据的逻辑结构描述数据元素之间的( ),与存储方式无关。

线性表L=(a1,a2,…,an)用数组表示,假定删除表中任一元素的概率相同,则删除一个元素平均需要移动元素的个数是( )

在长度为n的顺序表中删除第i(1≤i≤n)个结点,需要移动( )个结点。

( )是限定在表的一端进行插入和删除运算的线性表。

设线性表的长度为n,则顺序查找成功时的平均查找长度为( )

图的存储结构主要有( )和邻接表。

称算法的时间复杂度为O(f(n)),其含义是指算法的执行时间和 ( )的数量级相同。

队列的队尾位置通常是随着( )操作而变化的。

对于n个结点的无向图,采用邻接矩阵表示,求图中边数的方法是邻接矩阵中1的个数除以2,判断任意两个顶点i和j是否有边相连的方法是( ),求任意一个顶点的度的方法是( )

在有向图G的拓扑序列中,若顶点v在顶点v之前,则下列情形不可能出现的是【】

以下关于图的存储结构的叙述中正确的是【】

在双向链表中某结点(已知其地址)前,插人一新结点,其所需时间为【】

设二维数组a[10][20]按列优先存储在内存中,假设每个元素占3个存储单元,已知a[45]的存储单元地址为500,则a[8][7]的存储单元地址为【】

对长度为n的关键字序列进行堆排序的空间复杂度为【】

允许对队列进行的操作有【】

语句for(i=1i<=ni++)x++;的时间复杂度为【】

设单链表的长度为n,则删去第i(1≤i≤n)个结点的算法的时间复杂度为【】

设广义表L=((a,b,c)),则L的长度和深度分别为【】

下面不属于数据的存储结构的是【】

已知含10个结点的二叉排序树是一棵完全二叉树,则该二叉排序树在等概率情况下查找成功的平均查找长度等于【】

对一个表长为n的线性表采用顺序查找,在等概率情况下,查找成功的平均查找长度是【】

下面程序段的时间复杂度是【】

for(i=0;

i<2*n;i++)for(j=1j<3n;

j++)A[ij]=0;

二维数组A的每个元素占6个字节,其行下标i=0,1,…,8,列下标j=1,2,10若A按行优先存储,元素A[8,5]的起始地址与当A按列优先存储时的元素【】的起始地址相同。

顺序存储的线性表(a1,a2,…,an),在任一结点前插入一个新结点时所需移动结点的平均次数为【】