自考计算机网络数据结构模拟试卷五
-
设A和B是两个单链表,其表中元素递增有序。试写一算法将A和B归并成一个按元素值递减有序的单链表C,并要求辅助空间为O(1),请分析算法的时间复杂度。
-
下面函数 CreateList()的功能是用头插法建立单链表。请在空缺处填写相应的语句
LinkList CreatList()
LinkList head;
ListNode *p;
char ch;
head=NULL;//置空单链表
ch=getchar();//读入第一个字符
while(ch!='\n'){ //读人字符不是结束标志符时作循环
p=(ListNode malloc( sizeof(ListNode));//申请新结点
p->data= (1) //数据域赋值
p->next=head;//指针域赋值
(2) ;//头指针指向新结点
ch= (3) //读入下一个字符
}
return head;//返回链表的头指针
(1)
(2)
(3)
-
下列函数的功能是:对以带头结点的单链表作为存储结构的两个递增有序表(表中不存在值相同的数据元素)进行如下操作:将所有在Lb表中存在而La表中不存在的结点插入到La中,其中La和Lb分别为两个链表的头指针请在空缺处填人合适内容,使其成为一个完整的算法
void union (LinkList La, LinkList Lb)
{
//本算法的功能是将所有Lb表中存在而La表中不存在的结点插入到La表中
LinkList pre=La,
LinkList pa-La->next;
LinkList pb=Lb->next;
free(Lb);
while (pa &&pb)
{
if (pa->data
data) pre=pa; pa-pa->next;)
else if (pa->data>pb->data)
{
(1) ;
pre=pb;
pb=pb->next;
(2) ;
}
Else
{
q-pb: pb=pb->next; free(q);
}
}
if (pb)
(3) ;
}
(1)
(2)
(3)
-
已给如下关于单链表的类型说明:
typedef struct node
int data;
struct node *next;
}listnode, *list;
以下程序采用链表合并的方法,将两个已排序的不带头结点的单链表合并成一个链表而不改变其排序性(升序),这里两个链表的头指针分别为p和q。请将算法补充完整。
void mergelink(list p, list q)
{
list h,;
h=(listnode *)malloc(sizeof(listnode));
h->next=NULL; r=h;
while(p&&q)
if (p->data<=q->data)
(1); r=p: p=p->next;)
else
{(2); r=q; q-q>next;)
if (!p)r->next=q;
if(q)(3);
p=h->next; free();
}
(1)
(2)
(3)
-
如果希望循环队列中的存储单元都能得到利用,则可设置一个标志域tag,每当尾指针和头指针值相同时,以tag的值为0或1来区分队列状态是“空”还是“满”。请对下列函数填空,使其分别实现与此结构相应的入队列和出队列的算法。
int EnQueue(CirQueue*Q, DataType x)
{
if(Q>tag==)return 0;
Q->data[Q->rear]=;
Q->rear=(Q>rear+1)% QueueSize;
if(-qfront)q→>tag=1
return 1;
}
int DeQueue( CirQueue *, DataType x)
if( (1) ) return;
*x-Q->data[Q>front];
Qfront (2)
(3) ;
return 1;
}
(1)
(2)
(3)
-
要在[on-1]的向量空间中建立两个栈 stackl和 stack22,请回答
(1)应该如何设计这两个栈才能充分利用整个向量空间?
(2)若的顶指针为topl l, stack的顶指针为top2,如果需要充分利用整个向量空间,则栈 stackl空的条件是:栈 stack2空的条件是:栈 stackI和栈 stack2满的条件是:
-
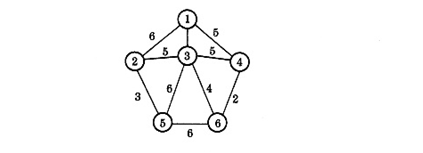
画出题图采用普里姆(Prim)算法构造最小生成树的全过程。
-
设有序表为(a,b,c,d,e,f,g,i,j,k,p,q),请分别画出对给定值b和n进行折半查找的过程。
-
(1)画出对表长为13的有序顺序表进行二分查找的判定树。
(2)已知关键字序列为(12,14,16,21,24,28,3,43,52,67,71,84,99),写出在该序列中二分查找37时所需进行的比较次数。
-
设广义表L(,()),则tail(L)= ( )
-
链接存储的特点是利用( )来表示数据元素之间的逻辑关系。
-
广义表LS=(a1,a2,…,an),其长度为( )
-
设某非空双链表,其结点形式为prior data next若要删除指针q所指向的结点,则需执行下述语句段:q->prior-->nextq-->next;( )
-
有向图中的极大连通子图称作有向图的( )
-
迪杰斯特拉提出了按( )递增的顺序产生诸顶点的最短路径算法。
-
下面算法的时间复杂度为( )
void fun(int n){int i,j,=;
for (i=1;
ifor (j=n;j>=i+1;j--)x++}
-
线性结构中,有且仅有一个开始结点和一个( )
-
开放定址法分为线性探查法、二次探查法和( )三种
-
栈的两种常用存储结构分别为【】
- A.顺序存储结构和链式存储结构
- B.顺序存储结构和散列存储结构
- C.链式存储结构和索引存储结构
- D.链式存储结构和散列存储结构
-
一个栈的输入序列为1,2,3,…,n,若输出序列的第一个元素是n,输出第i(1≤i≤n)个元素是【】
- A.不确定
- B.n-i+1
- C.i
- D.n-i
-
设顺序栈存放在s.data[maxsize]中,底位置是maxsize-1,则栈空条件是( )栈满条件是( )
-
栈的特点是【】
- A.先进先出
- B.后进后出
- C.后进先出
- D.随意进出
-
采用邻接表存储的图的广度优先遍历算法类似于二叉树的【】
- A.按层遍历
- B.前序遍历
- C.后序遍历
- D.中序遍历
-
对于一个具有n个顶点的无向图,若采用邻接矩阵表示,该矩阵的大小为【】
- A.n
- B.n+1
- C.n'
- D.(n-1)2
-
采用分块查找时,若线性表中共有625个元素,查找每个元素的概率相同,假设采用顺序查找来确定结点所在的块,则每块分为【】个结点最佳。
- A.9
- B.25
- C.6
- D.625
-
线性结构的数据元素之间存在着【】的关系。
- A.一对一
- B.一对多
- C.多对一
- D.多对多
-
二叉树和度为2的树的相同之处包括【】
- A.每个结点都有一个或两个孩子结点
- B.至少有一个根结点
- C.至少有一个度为2的结点
- D.每个结点至多只有一个双亲结点
-
下面有关图的相关概念说法正确的是【】
- A.有e条边的无向图,在邻接表中有e个结点
- B.有向图的邻接矩阵是对称的
- C.任何无向图都存在生成树
- D.不同的求最小生成树的方法最后得到的最小生成树的权值之和是相等的
-
若二叉树的中序遍历序列是 abedef,且c为根结点,则【】
- A.结点c有两个孩子
- B.二叉树有两个度为0的结点
- C.二叉树的高度为5
- D.以上都不对
-
用单链表表示的链队中,队头在链表的【】位置。
- A.链头
- B.链尾
- C.链中
- D.以上都可以
-
下列排序方法中不稳定的为【】
- A.冒泡排序
- B.直接选择排序
- C.直接插入
- D.归并排序
-
图的广度优先遍历算法用到一个队列,每个顶点多最多进队【】次。
- A.1
- B.2
- C.3
- D.不确定
-
完成在双向循环链表结点p之后插入新结点s的操作是【】
- A.p->next=ss->prior=p;p>next>priorssnextp->next;
- B.p->next->prior=s; p->next= s; s->prior=; s->next=p->next;
- C.s->prior=; s->next=p->next; p->next=s; p->next->prior=s;
- D.>prior=p; s->next=p->next; p->next->prior-s; p->next=s;
-
假设散列表m=11,散列函数h(key)=key%11.表中已有4个结点:h(39)=6,h(41)8,h(53)=9,h(76)=10占了4个地址位置,其余地址为空,如果用线性探查法处理冲突,存储关键字为85需要探查的次数是【】
- A.2
- B.3
- C.4
- D.5
