自考专业课运筹学基础模拟试卷七

某厂考虑生产甲乙两种产品,根据对过去市场需求的统计,可知不同需求状态出现的概率及相应的获利情况如下表所示:

(1)做出决策树;

(2)用期望收益值标准进行决策。

用图解法求下述线性规划问题,并说明在最优解处哪些约束成为等式

Max 8X1+6X2s.t.2x1+x2≤30

(1)2X1+3x2≤36

(2)X1≥0(3)X2≥0(4)

如图是五个城市之间的公路所能承受的最大流量,以每小时1000辆汽车计算,求V到V之间的最大流量及安排。

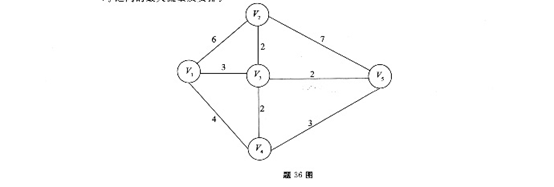
某单位搞农业开发。设想有三种方案,有三种自然状态,其收益预测如下表:

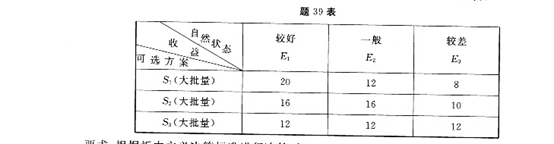
要求:根据折中主义决策标准进行决策时:

(1)折中系数a=0.6时的最优方案是哪种

(2)折中系数a在什么范围内取值时,S1为最优方案。

设有某项活动,采用正常的工艺方法,施工周期为7周,对应的施工费用为14000元,若对该活动进行赶工,使施工周期缩短为4周,则对应的施工费用为17000元。计算该活动的施工费用增长率。

某项活动,按最先进、最可能最保守的估计,完成时间分别为31天、37天、43天,按三项时间估计法,计算该活动的作业时间T

经济订货量

存货台套法

保管费用

定量决策

时间优化

悲观主义原则也称( )原则,乐观主义原则也称( )原则。

求得运输问题的一个最初方案,常用方法是西北角法,也叫做()

再订货点有两种含义,一个是( )上的含义,一个是( )上的含义。

库存费用基本上可以分为()和()

箭线式网络图的结点不( ),不( )

在一个树上任添一边,则树( ),任减一边,则树( )

运输问题肯定有()解,由于约束方程的结构,它不存在()解的可能。

在一棵树中,()数目比()的数目多1

单纯形法是解( )问题的一种简单方法,它通过( )过程,逐步求得最优解。

企业价格预测就是在的基础上,为企业()提供适当的数据和资料

在箭线式网络图中,活动i→j的最迟完成时间LFi,j等于()

• A.ESj
• B.LSi,j
• C.LFj
• D.ESi+Ti,j

最迟完成时间LF的计算公式为()

• A.LFi=min{LFi-Tj}
• B.LFi=max(LFj+Ti)
• C.LFi=min(LFj+TI,j.)
• D.LFi=max(LFi-Ti,j.)

库存管理中,只要求做到不缺货、不影响生产,而不必过分细致管理的存货是()

• A.A类
• B.B类
• C.C类
• D.B类和C类

设自变量为x1,x2,因变量为y,则二元线性回归模型的一般公式为()

• A.y=a+b1x1+b2x2
• B.y=a+x1+x2
• C.y=a+bx1x2
• D.y=ax1x2

P为任一概率矩阵,Q为一固定概率矩阵,则P()

• A.必为一固定概率矩阵
• B.可能不是固定概率矩阵
• C.是一可逆矩阵
• D.不等于Q

进行成本最小化决策时,悲观主义者的决策原则将是()

• A.最小最小原则
• B.最小最大原则
• C.最大最大原则
• D.最大最小原则

下列哪个决策原则也被称为悲观主义原则

• A.最大最小原则
• B.最大最大原则
• C.风险期望原则
• D.最小最大遗憾原则

下列说法中,不正确的是()

• A.图是反映对象之间关系的一种工具
• B.图的基本要素是点和线
• C.连通的图一定是树
• D.图中的点代表研究的对象

对于线性规划问题:maxS=100X+80x2,约束为x1+4x2≤80,3x1+x2≤60,x1,()≥0,其最优解为

• A.1=16,X212
• B.1=20,X2=0
• C.X2=20,X1=0
• D.X1=12,X2-16

A、B、C、D四人要进行单独面谈,任两人必至少有一次谈话机会,用来表示这一情况的图是()

• A.一棵树
• B.没有圈
• C.连通的
• D.任两点之间有一条带方向的箭头

某存货台套占存货总单元数的30%,年度需用价值的20%,则该存货台套属于()

• A.A类存货
• B.B类存货
• C.C类存货
• D.ABC类存货

T为任一概率向量,P为任一概率矩阵,当n趋于+∞时,成立的是()                            

• A.TP是任意向量
• B.TP是一个固定的向量
• C.TP是零向量
• D.TP是一单位向量

依据事物发展的内部因素变化的因果关系来预测事物未来的发展趋势,这种定量预测方法属于()

• A.指数平滑预测法
• B.回归模型预测法
• C.专家小组法
• D.特尔斐法

设A方案在状态下的收益值为f(A,0),遗憾值为R(A,),则最小最大遗憾原则可表述为()

• A.[ R(A,Q)]
• B.[ RR(A,Q)]
• C.[ Rf(A,Q)]
• D.[ f(A,Q)]

在下面的无向网络图中,节点连线上的数字为它们之间的距离,则节点1到节点5之间的最短距离是()

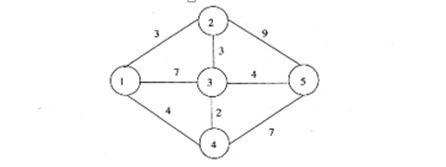
• A.9
• B.10
• C.11
• D.12