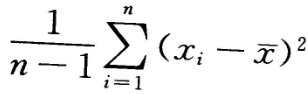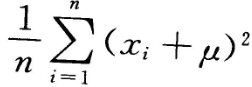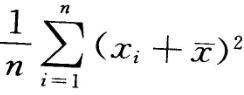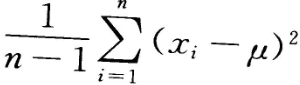全国概率论与数理统计(经管类)考前模拟试题八
-
设一个系统由100个相互独立作用的部件组成,每个部件损坏的概率为0.1,必须有85个以上的部件正常工作,才能保证系统正常运行,求整个系统正常工作的概率.
-
设随机变量X服从[0,1]上的均匀分布,Y服从参数为5的指数分布,且X与Y独立。
(1)二维随机变量(X,Y)的概率密度。
(2)P{X>Y}
-
设二维随机变量(X,Y)的概率密度为
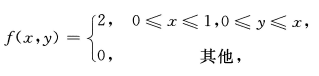
求:
(1)E(XY)
(2)
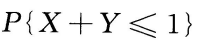
-
某种电器元件的寿命服从指数分布,其平均寿命为100小时,各元件之间的使用情况是独立的,利用中心极限定理,求16只这样的元件的寿命总和大于1920小时的概率。
(附:
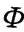 (0.8)=0.788,
(0.8)=0.788,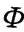 (0.9)=0.815)
(0.9)=0.815) -
A、B为两事件,若已知P(A)=0.92,P(B)=0.93,
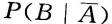 =0.85。
=0.85。求:
(1)P(AB)
(2)P(AUB)
-
若P(A)=0.7,P(A-B)=0.3,则P(
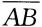 )=______。
)=______。 -
当a=0.01时,犯第一类错误的概率不超过 _________.
-
设二维随机变量(X,Y)的分布律为
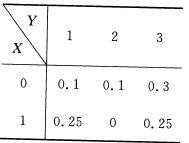
则
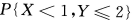 =______。
=______。 -
若X~N(0,1),Y~N(0,2)且X与Y独立,则X+Y?
-
某地区成年人患A,B两种病的概率分别为0. 015和0. 08,设这两种病的发生量是相互独立的,则该地区任一成年人同时患有这两种病的概率为_________.
-
若X的分布律为

则
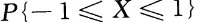 _____.
_____. -
设随机变量X服从参数为
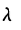 的泊松分布,且满足P{X=2}=P{X=3},则P{X=4}=______。
的泊松分布,且满足P{X=2}=P{X=3},则P{X=4}=______。 -
已知随机变量X的分布函数为
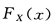 ,则随机变量Y=3X+2的分布函数
,则随机变量Y=3X+2的分布函数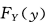 =______。
=______。 -
若X的概率密度为
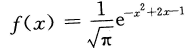 则X~________。
则X~________。 -

-
设随机变量X的概率密度为
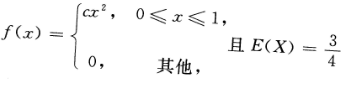 ,则c=()
,则c=()- A.2
- B.3
- C.1
- D.4
-
设随机变量X~N(0,1),Y~N(0,1),Z~N(0,1),且X、Y、Z相互独立,则
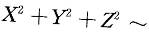 ()
()- A.N(0,3)
- B.
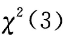
- D.F(1,1)
-
设随机变量X服从参数为1/4的指数分布,则E(X)=()
- A.1/4
- B.4
- C.1/16
- D.16
-
从总体X中抽取样本
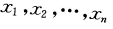 若E(X)=
若E(X)=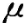 ,D(X)=
,D(X)=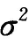 ,下列统计量中是
,下列统计量中是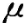 的无偏估计量的为()
的无偏估计量的为()- A.
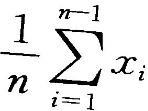
- B.
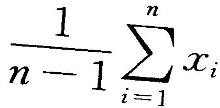
- C.
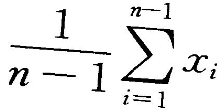
- D.
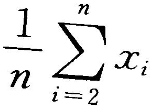
- A.
-
若随机变量X的分布律为
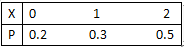 则P{
则P{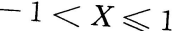 }=()
}=()- A.0.2
- B.0.7
- C.0.3
- D.0.5
-
已知随机变量X与Y相互独立,且它们分别在区间[―1,3]和[2,4]上服从均勻分布,则E(XY)=()
- A.3
- B.6
- C.10
- D.12
-
随机变量Y关于X的一元线性回归方程的一般形式为()
- A.
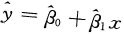
- B.
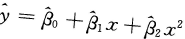
- C.
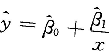
- D.
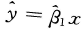
- A.
-
设样本
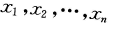 来自正态总体N
来自正态总体N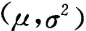 ,在进行假设检验时,下列哪种情况下,采用统计量
,在进行假设检验时,下列哪种情况下,采用统计量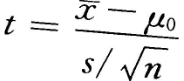 ()
()- A.
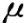 未知
未知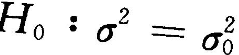
- B.
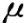 已知
已知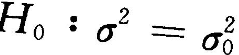
- C.
 未知
未知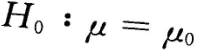
- D.
 已知
已知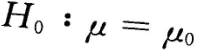
- A.
-
设二维随机变量(X,Y)的密度函数为
 则X与Y()
则X与Y()- A.独立且有相同分布
- B.不独立但有相同分布
- C.独立而分布不同
- D.不独立也不同分布
-
设总体X~N
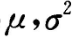 ,而
,而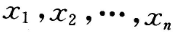 为来自总体X的样本,
为来自总体X的样本,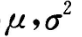 均未知,则
均未知,则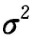 的无偏估计是()
的无偏估计是()- A.
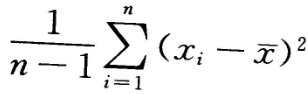
- B.
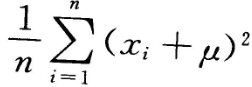
- C.
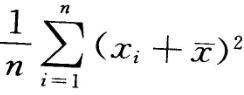
- D.
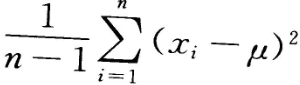
- A.
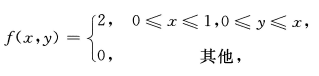



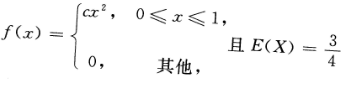 ,则c=()
,则c=()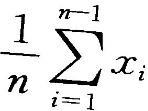
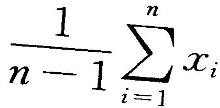
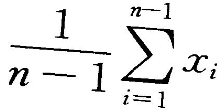
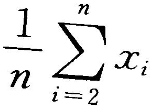
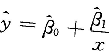
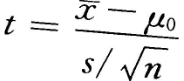 ()
()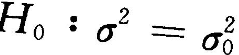
 则X与Y()
则X与Y()