全国概率论与数理统计(经管类)考前模拟试题七
-
设二维随机变量(X,Y)的分布律为
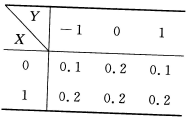
求:
(1)E(X),E(Y);
(2)D(X),D(Y);
(3)
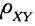 。
。 -

-
设二维随机变量(X,Y)的分布律为
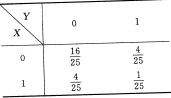
(1)E(X),E(Y),D(X),D(Y);
(2)Cov(X,Y);
(3)X与Y独立吗?
-
若X~B(2,p),已知
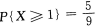 则p=________。
则p=________。 -
设总体X服从参数为
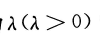 的指数分布,其概率密度为
的指数分布,其概率密度为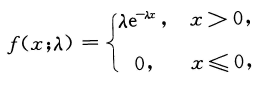
由来自总体X的一个样本
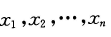 算得样本均值
算得样本均值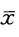 =5,
=5,则参数
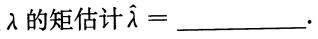
-
若P(A)=P(B)=P(C)=1/4,P(AB)=P(AC)=0,P(AC)=1/8,则A、B、C中至少有一个发生的概率为_____。
-
若随机变量x与y相互独立,其分布律分别为


则(X,Y)的分布律为______。
-
若X的分布律为
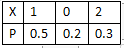
则E(X2)=________。
-
—元线性回归的数学模型为
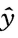 =_____。
=_____。 -
设随机变量X~N(2,4),且Y=3—2X,则D(Y)=______。
-
随机变量X的分布律为

则X的分布函数F(X)=________。
-
若估计量
 是未知参数
是未知参数 的无偏估计,则一定有
的无偏估计,则一定有 =________。
=________。 -
甲、乙两人独立地破译一份密码,若他们各人译出的概率均为0.25,则这份密码能破译出的概率为______.
-

- A.

- B.

- C.
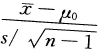
- D.

- A.
-
若二维随机变量(X,Y)服从D上的均匀分布,
 则
则 的概率密度为________。
的概率密度为________。 -

-
A与B相互独立,P(A)>0,P(B)>0,则一定有P(AUB)=()
- A.P(A)+P(B)
- B.P(A)P(B)
- C.

- D.

-
设随机变量X的分布函数为

则P{0.2
- A.0.01
- B.0.05
- C.0.1
- D.0.4
-
随机变量X的概率密度为f(x),则f(x)—定满足()
- A.

- B.f(x)为连续函数
- C.

- D.

- A.
-
设随机变量X和Y相互独立,且X~N(2,1),Y~N(3,2),则Z=3X—2Y~()
- A.N(1,36)
- B.N(0,17)
- C.N(0,36)
- D.N(1,25)
-
设总体X的概率密度为

 为来自X的样本,
为来自X的样本, 为样本均值,则参数
为样本均值,则参数 的无偏估计为()
的无偏估计为()- A.

- B.

- C.

- D.

- A.
-
设二维随机变量(X,Y)的分布律为

则P{X+Y-1}=()
- A.0.2
- B.0.3
- C.0.5
- D.0.4
-

- A.1
- B.1/2
- C.-1/2
- D.-1
-
设总体X服从[―1,1]上的均匀分布,
 为其样本,则样本均值
为其样本,则样本均值 的方差D(
的方差D( )=()
)=()- A.0
- B.1/3
- C.

- D.3
-
随机变量X与Y都服从[一1,1]上的均匀分布,则E:(X+Y)=()
- A.1
- B.0
- C.-1
- D.2



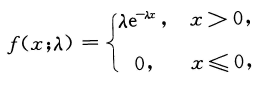






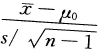




 为其样本,则样本均值
为其样本,则样本均值 的方差D(
的方差D(