概率论与数理统计(经管类)2018年10月真题
-
设X、Y为随机变量,已知E(X)=E(Y)=2,D(X)=D(Y)=1,
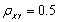 。求:
。求:(1)E(X-2Y);
(2)D(X-2Y);
(3)E(XY)。
-
将一颗骰子独立地投掷4次,观察出现的点数。事件A表示每次投掷“出现小于5的偶数点”。求:
(1)在4次投掷中,事件A恰好发生一次的概率P1;
(2)在4次投掷中,事件A恰好发生两次的概率P2;
(3)在4次投掷中,事件A至少发生一次的概率P3。
-
某厂生产一种元件,其直径X(单位:cm)服从正态分布N(3,0.12),现改换一种新工艺生产该元件,从新工艺生产的元件中随机抽取25个,测得样本均值
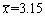 ,试判断用新工艺生产后,元件平均直径是否较以前有显著变化。(α=0.05,
,试判断用新工艺生产后,元件平均直径是否较以前有显著变化。(α=0.05,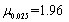 )
) -
设随机变量X的分布函数为
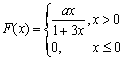
求:(1)常数a;(2)X的概率密度f(x)。
-
已知随机变量X、Y相互独立,X、Y的概率密度分别为
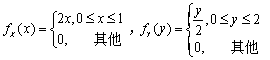
求:(1)(X,Y)的概率密度f(x,y);(2)
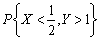 。
。 -
设
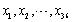 为来自总体X的样本,X~N(μ,1),已知样本均值
为来自总体X的样本,X~N(μ,1),已知样本均值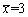 ,则μ的置信度为0.90的置信区间为________。(
,则μ的置信度为0.90的置信区间为________。(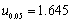 )
) -
依据样本
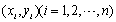 得到一元线性回归方程
得到一元线性回归方程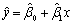 ,
,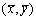 为样本均值。令
为样本均值。令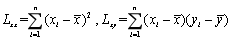 ,则
,则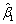 =________。
=________。 -
设随机变量X、Y满足E(X)=2,E(Y)=2,E(XY)=4,则Cov(2X,Y)=________。
-
设
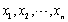 为来自总体X的样本,
为来自总体X的样本,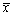 为样本均值,X在区间[0,θ]上服从均匀分布,θ>0,则未知参数θ的矩估计
为样本均值,X在区间[0,θ]上服从均匀分布,θ>0,则未知参数θ的矩估计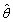 =________。
=________。 -
设总体X~N(μ,32),
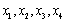 为来自X的样本,s为样本方差,则E(s2)=________。
为来自X的样本,s为样本方差,则E(s2)=________。 -
设随机变量X,Y相互独立,且X~B(18,1/3),Y服从参数为4的泊松分布,则D(X-Y)=________。
-
设随机变量X的概率密度为
 ,则E(X)=________。
,则E(X)=________。 -
设二维随机变量(X,Y)的分布律为

则P{X+Y>2}=________。
-
设随机变量X在区间[1,6]上服从均匀分布,P{2
-
设随机变量X、Y独立同分布,且X~B(1,1 /4),则P{X+Y=2}=________。
-
设随机变量X的概率密度为
 ,则P{2X>1} =________。
,则P{2X>1} =________。 -
设随机变量X的分布律为
 ,则P{X2=9}=________。
,则P{X2=9}=________。 -
设随机变量X~N(3,42),Y=2X+1,则Y~________。
-
设A、B为随机事件,且P(A)=0.5,P(AB)=0.3,则P(B|A)=________。
-
设A,B为相互独立的随机事件,P(A)=0.3,P(B)=0.4,则
 =________。
=________。 -
设总体X~N(μ,σ2),
 为来自X的样本,
为来自X的样本, 为样本均值,s2为样本方差,则下列结论成立的是()
为样本均值,s2为样本方差,则下列结论成立的是()- A.
 为μ的无偏估计
为μ的无偏估计 - B.(n-1)s2为σ2的无偏估计
- C.
 为μ的无偏估计
为μ的无偏估计 - D.s为σ的无偏估计
- A.
-
设总体X~N(μ,σ2),
 为来自该总体的样本,
为来自该总体的样本, 为样本均值,则
为样本均值,则 服从的分布是( )
服从的分布是( )- A.N(μ,σ2)
- B.N(nμ,σ2)
- C.N(μ,σ2/n)
- D.N(μ,nσ2)
-
设
 是来自总体X的样本,且X~N(0,1),则
是来自总体X的样本,且X~N(0,1),则 服从的分布是( )
服从的分布是( )- A.χ2(9)
- B.χ2(10)
- C.t(9)
- D.t(10)
-
设随机变量X、Y独立同分布,且X的分布律为
 ,则E(XY)=( )
,则E(XY)=( )- A.0
- B.3/7
- C.7/3
- D.49/9
-
设二维随机变量(X,Y)的概率密度为
 ,则常数c=( )
,则常数c=( )- A.1/4
- B.1/2
- C.3
- D.4
-
设随机变量X~B(3,1 / 5),则P{X=2}=( )
- A.1/125
- B.12/125
- C.3/25
- D.12/25
-
设二维随机变量(X,Y)的分布律为

则P{X=0} =( )
- A.0.1
- B.0.2
- C.0.3
- D.0.5
-
设随机变量X在[-2,2]上服从均匀分布,则P{X≥1}=( )
- A.0
- B.1/4
- C.1/2
- D.1
-
设事件A、B互不相容,且P(A)=0.2,P(B)=0.3,则P(A∪B)=( )
- A.0.2
- B.0.3
- C.0.5
- D.0.56
-
有6部手机,其中4部是同型号甲手机,2部是同型号乙手机,从中任取3部,恰好取到一部乙手机的概率是( )
- A.1/20
- B.1/10
- C.3/10
- D.3/5
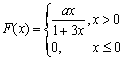
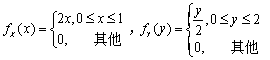

 ,则P{X2=9}=________。
,则P{X2=9}=________。 为来自该总体的样本,
为来自该总体的样本, ,则E(XY)=( )
,则E(XY)=( ) ,则常数c=( )
,则常数c=( )