概率论与数理统计(经管类)2015年10月真题
-
在某次考试中,随机抽取16位考生的成绩,算得平均成绩为
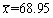 。若设这次考试成绩X~N(μ,16),在显著性水平α=0.05下,可否认为全体考生的平均成绩为70分?(附:
。若设这次考试成绩X~N(μ,16),在显著性水平α=0.05下,可否认为全体考生的平均成绩为70分?(附: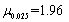 )
) -
设随机变量X~N(-2,4),Y服从区间[-2,0]上的均匀分布。
求:(1) 当X与Y相互独立时,求E[(XY)2];
(2) 当X与Y的相关系数
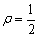 时,求Cov(2X,Y)。
时,求Cov(2X,Y)。 -
箱中装有10件产品,其中8件正品,2件次品,从中任取2件,x表示取到的次品数。
求:(1)X的分布律;
(2)X的分布函数F(x);
(3)P{0
-
设总体X服从区间[1,θ]上的均匀分布,其中θ未知,且θ>1,
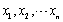 为来自总体X的一个样本,
为来自总体X的一个样本,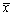 为样本均值。
为样本均值。求:(1)θ的矩估计
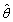 ;(2)讨论
;(2)讨论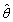 的无偏性。
的无偏性。 -
设某总体X的样本为
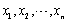 ,D(X)=σ2,则
,D(X)=σ2,则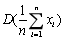 =________。
=________。 -
已知甲袋中有3个白球、2个红球;乙袋中有1个白球、2个红球。现从甲袋中任取一球放入乙袋,再从乙袋中任取一球,求该球是白球的概率。
-
设X~N(0,1),Y~X2(10),且X与Y相互独立,则
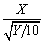 ~________。
~________。 -
在贝努利试验中,若事件A发生的概率为p(0
Φ(X)为标准正态分布函数,则
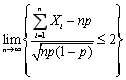 =________。
=________。 -
设X~B(5,1/5),则D(X)=________。
-
设随机变量X与Y的协方差Cov(X,Y)=-1/2,E(X)=E(Y)=1,则E(XY)=________。
-
设二维随机变量(X,Y)服从区域D:0≤x≤4,0≤y≤4上的均匀分布,则
 =________。
=________。 -
设X在区间[1,4]上服从均匀分布,则E(X)=________。
-
设二维随机变量(X,Y)的分布函数为F(x,y),则P{X≤0,Y≤0}用F(x,y)表示为________。
-
设二维随机变量(X,Y)服从区域D:-1≤x≤2,0≤y≤2上的均匀分布,则(X,Y)的概率密度f(x,y)在D上的表达式为________。
-
设二维随机变量(X,Y)的分布律为

则c=________。
-
设随机变量X服从参数为1的指数分布,则P{X>2}=________。
-
设X表示某射手在一次射击中命中目标的次数,该射手的命中率为0.9,则P{x=0} =________。
-
设事件A,B相互独立,且P(A)=0.3,P(B)=0.4,则
 = ________。
= ________。 -
设A、B为随机事件,则事件“A,B至少有一个发生”可由A,B表示为________。
-
设a是假设检验中犯第一类错误的概率,
 为原假设,以下概率为a的是( )
为原假设,以下概率为a的是( )- A.

- B.

- C.

- D.

- A.
-
袋中有编号为0,1,2,3,4的5个球。今从袋中任取一球,取后放回;再从袋中任取一球,则取到两个0号球的概率为________。
-
已知X与Y的协方差Cov(X,Y)=-1/2,则Cov(-2X,Y)=( )
- A.-1/2
- B.0
- C.1/2
- D.1
-
设
 为总体X的一个样本,且E(X)=μ(未知),
为总体X的一个样本,且E(X)=μ(未知), 为样本均值,则μ的无偏估计为( )
为样本均值,则μ的无偏估计为( )- A.

- B.

- C.

- D.

- A.
-
设随机变量X服从参数为3的泊松分布,Y服从参数为1/5的指数分布,且X、Y相互独立,则D(X-2Y+1)=( )
- A.23
- B.28
- C.103
- D.104
-
设随机变量X~N(3,22),则E(2X+3)=( )
- A.3
- B.6
- C.9
- D.15
-
设二维随机变量(X,Y)的分布律为

则P{X=1} =( )
- A.0.1
- B.0.2
- C.0.3
- D.0.4
-
设随机变量X的分布律为
 ,则P{X2=1}=( )
,则P{X2=1}=( )- A.0.2
- B.0.4
- C.0.6
- D.0.8
-
设随机变量X的概率密度为
 ,则常数a=( )
,则常数a=( )- A.0
- B.1/3
- C.1/2
- D.3
-
设随机变量X~B(3,0.3),则P{X=2}=( )
- A.0.189
- B.0.21
- C.0.441
- D.0.7
-
设事件A与B互不相容,且P(A)=0.4,P(B)=0.2,则P(A∪B)=( )
- A.0
- B.0.2
- C.0.4
- D.0.6
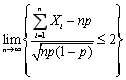 =________。
=________。
