概率论与数理统计(经管类)2015年4月真题
-
设一台自动车床加工零件其长度X(单位:厘米)服从正态分布N(μ,0.16),现从加工出的零件中随机抽取16个进行测量,并算得平均值
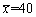 ,求μ的置信度为0.95的置信区间。(附:
,求μ的置信度为0.95的置信区间。(附: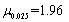 )
) -
设二维随机变量(X,Y)的分布律为

求:(1)E(X),E(Y);
(2)D(X),D(Y);
(3)Cov(X,Y),
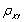 。
。 -
设随机变量X服从[0,1]上的均匀分布,随机变量Y的概率密度
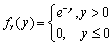 且X与Y相互独立。
且X与Y相互独立。求:(1)X的概率密度
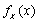 ;
;(2)(X,Y)的概率密度f(x,y);
(3)P{X+Y≤1}。
-
设连续型随机变量X的分布函数为
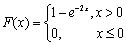 ,其概率密度为f(x)。
,其概率密度为f(x)。求:(1)f(3);
(2)P{X>3}。
-
设一元线性回归数学模型为
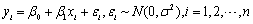 ,且各
,且各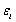 相互独立,记
相互独立,记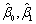 分别为
分别为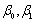 的最小二乘估计,则一元线性回归方程是
的最小二乘估计,则一元线性回归方程是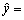 ________。
________。 -
盒中有4个白球,2个红球。从中连续不放回地取两次,每次取1个球。求第二次取到红球的概率。
-
设某产品的一项指标X~N(μ,σ2),σ2未知,
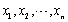 是对X的n(n>1)次独立观测值,记
是对X的n(n>1)次独立观测值,记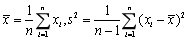 ,则假设
,则假设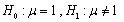 的检验统计量表达式为________。
的检验统计量表达式为________。 -
设总体X~U(0,2θ),θ>0,
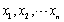 为来自X的样本,
为来自X的样本,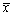 为样本均值,则未知参数θ的矩估计
为样本均值,则未知参数θ的矩估计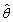 =________。
=________。 -
设总体X~N(μ,σ2),检验假设
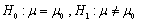 ,μ0已知,给定检验水平α,则拒绝H0的可信度为________。
,μ0已知,给定检验水平α,则拒绝H0的可信度为________。 -
设随机变量X的方差D(X)存在,则对任意小正数ε,P{|X-E(X)|<ε}≥________。
-
设
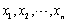 为来自正态总体N(1,4)的样本,则
为来自正态总体N(1,4)的样本,则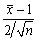 ________。
________。 -
设随机变量X与Y相互独立,X服从区间[-2,2]上的均匀分布,Y服从参数为1的指数分布.则当-20时,(X,Y)的概率密度f(x,y)=________。
-
设随机变量X服从参数为λ的泊松分布,E(X)=5,则λ=________。
-
设随机交量X与Y相互独立,且X~N(2,4),Y~U(-1,3),则E(XY)=________。
-
设随机变量X与Y相互独立,且
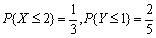 ,则P{X≤2,Y≤1}=________。
,则P{X≤2,Y≤1}=________。 -
设随机变量X服从区间[a,b]上的均匀分布,则当a
-
设随机变量X的分布律为
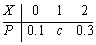 ,则常数c=________。
,则常数c=________。 -
设A,B为随机事件,且P(A)=0.6,P(B)=0.3,P(B|A)=0.2,则P(AUB)=________。
-
设某射手命中率为0.7,他向目标独立射击3次,刚至少命中一次的概率为________。
-
设总体X~N(μ,σ02),σ02已知,
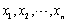 为来自X的样本,
为来自X的样本,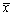 是样本均值。假设
是样本均值。假设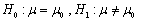 已知,检验统计量
已知,检验统计量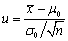 ,给定检验水平α,则拒绝H0的理由是( )
,给定检验水平α,则拒绝H0的理由是( )- A.
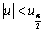
- B.
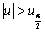
- C.
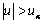
- D.

- A.
-
设事件A与B相互独立,P(A)=0.3,P(B)=0.5,则P(AB)=________。
-
设
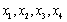 是来自总体X的样本,若E(X)=μ(未知),记
是来自总体X的样本,若E(X)=μ(未知),记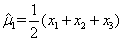
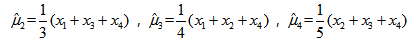 ,则μ的无偏估计是( )
,则μ的无偏估计是( )- A.
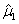
- B.
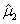
- C.
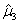
- D.
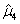
- A.
-
设总体X服从正态分布N(0,1),
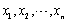 是来自X的样本,则
是来自X的样本,则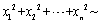 ( )
( )- A.N(0,1/n)
- B.N(0,1)
- C.χ2(n)
- D.t(n)
-
设随机变量X服从参数为1/2的指数分布,则E(2X-1)=( )
- A.0
- B.1
- C.3
- D.4
-
设随机变量X与Y的相关系数为0.5,D(X)=9,D(Y)=4,则D(3X-Y)=( )
- A.5
- B.23
- C.67
- D.85
-
设二维随机变量(X,Y)的分布律为

则P{X=Y} =( )
- A.0.2
- B.0.25
- C.0.3
- D.0.5
-
设随机变量X的分布函数为F(x),则下列结论中不一定成立的是( )
- A.F(-∞)=0
- B.F(+∞)=1
- C.0≤F(x)≤1
- D.F(x)是连续函数
-
设随机变量X的概率密度为
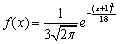 ,则X~( )
,则X~( )- A.N(-1,3)
- B.N(-1,9)
- C.N(0,3)
- D.N(1,9)
-
设随机变量X~B(3,0.2),则P{X>2}=( )
- A.0.008
- B.0.488
- C.0.512
- D.0.992
-
设A、B为随机事件,且P(AB)>0,则
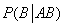 =( )
=( )- A.1
- B.P(A)
- C.P(B)
- D.P(AB)

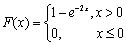 ,其概率密度为f(x)。
,其概率密度为f(x)。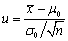 ,给定检验水平α,则拒绝H0的理由是( )
,给定检验水平α,则拒绝H0的理由是( )