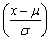概率论与数理统计(经管类)2013年10月真题
-
设随机变量X的概率密度为

求:(1)常数c;(2)X的分布函数F(x);(3)
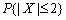
-
某保险公司有一险种,每个保单收取保险费600元,理赔额10000元,在有效期内只理赔一次。设保险公司共卖出这种保单800个,每个保单理赔概率为0.04。 求:
(1)理赔保单数的分布律;
(2)保险公司在该险种上获得的期望利润。
-
设某人群中患某种疾病的比例为20%。对该人群进行一种测试,若患病则测试结果一定为阳性;而未患病者中也有5%的测试结果呈阳性。求:
(1)测试结果呈阳性的概率;
(2)在测试结果呈阳性时,真正患病的概率。
-
假设某校数学测验成绩服从正态分布,从中抽出20名学生的分数,算得样本标准差s=4分,求正态分布方差σ2的置信度为98%的置信区间。

-
依据样本
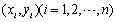 得到一元线性回归方程
得到一元线性回归方程 为样本均值,令
为样本均值,令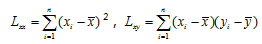 ,则回归常数
,则回归常数 =________。
=________。 -
设二维随机变量(X,Y)的概率密度为

求:(1)(X,Y)关于X,Y的边缘概率密度;
(2)P{X+Y≤2}。
-
设总体
 ,其中
,其中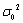 已知,
已知,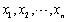 为来自X的样本,
为来自X的样本, 为样本均值,则对假设
为样本均值,则对假设 应采用的检验统计量的表达式为________。
应采用的检验统计量的表达式为________。 -
设随机变量t~t(n),且
 ,则
,则 =________。
=________。 -
设总体
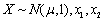 是来自X的样本.
是来自X的样本. 都是
都是 的估计量,则其中较有效的是________。
的估计量,则其中较有效的是________。 -
设总体X~N(0,1),x1、x2、x3为来自X的样本,则
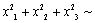 ________。
________。 -
设X为随机变量,E(X)=1,D(X)=0.5,则由切比雪夫不等式可得
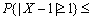 ________。
________。 -
设随机变量相互独立
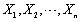 ,
,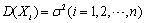 ,则
,则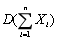 =________。
=________。 -
设随机变量X服从区间[0,2]上的均匀分布,则E(X)=________。
-
设随机变量X与Y的协方差Cov(X,Y)=-1,则Cov(2Y,-3X)=________。
-
设二维随机变量(X,Y)的分布函数为F(x,y),则F(+∞,-∞)=________。
-
设随机变量X与Y相互独立,且都服从参数为1的泊松分布,则P{X=1,Y=2}=________。
-
设随机变量X~N(1,1),Y=X-1,则Y的概率密度
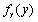 =________。
=________。 -
设随机变量X服从参数为1的指数分布,则P{X>1}=________。
-
甲、乙两个气象台独立地进行天气预报,它们预报准确的概率分别是0.8和0.7,则在一次预报中两个气象台都预报准确的概率是________。
-
设H0为假设检验的原假设,则显著性水平α等于()
- A.P{接受H0|H0不成立}
- B.P{拒绝H0|H0成立}
- C.P{拒绝H0|H0不成立}
- D.P{接受H0|H0成立}
-
设总体X~N(μ,σ2),其中σ2未知,
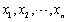 为来自X的样本,
为来自X的样本,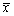 为样本均值,s为样本标准差。在显著性水平α下检验假设
为样本均值,s为样本标准差。在显著性水平α下检验假设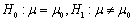 。令
。令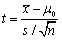 ,则拒绝域为()
,则拒绝域为()- A.
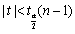
- B.
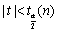
- C.
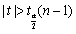
- D.

- A.
-
设随机事件A与B相互独立,且
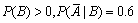 ,则P(A)=________。
,则P(A)=________。 -
设
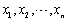 是来自正态总体N(μ,σ2)的样本,其中μ未知,
是来自正态总体N(μ,σ2)的样本,其中μ未知,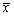 为样本均值,则σ2的无偏估计量为()
为样本均值,则σ2的无偏估计量为()- A.
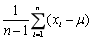
- B.
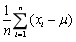
- C.
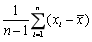
- D.
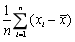
- A.
-
设总体X服从[0,θ]上的均匀分布(参数θ未知),
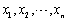 为来自X的样本,则下列随机变量中是统计量的为()
为来自X的样本,则下列随机变量中是统计量的为()- A.
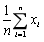
- B.
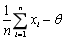
- C.
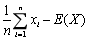
- D.

- A.
-
设随机变量X~B(n,p),且E(X)=2.4,D(X)=1.44,则()
- A.n=4,p=0.6
- B.n=6,p=0.4
- C.n=8,p=0.3
- D.n=24,p=0.1
-
设随机变量X~N(μ,σ2),Y服从参数为λ(λ>0)的指数分布,则下列结论中不正确的是()
- A.
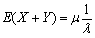
- B.

- C.
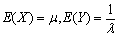
- D.
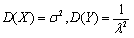
- A.
-
设二维随机变量(X,Y)的分布律为
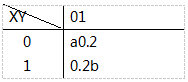
且P{Y=1|X=0}=0.5,则()
- A.a=0.2,b=0.4
- B.a=0.4,b=0.2
- C.a=0.1,b=0.5
- D.a=0.5,b=0.1
-
设二维随机变量
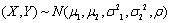 ,则X~()
,则X~()- A.
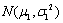
- B.
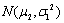
- C.
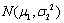
- D.

- A.
-
设随机变量X~N(μ,σ2),Φ(x)为标准正态分布函数,则P{X>x}=()
- A.Φ(x)
- B.1-Φ(x)
- C.Φ
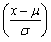
- D.1-Φ
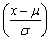
-
设A,B为随机事件,则事件“A,B至少有一个发生”可表示为()
- A.AB
- B.

- C.
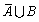
- D.A∪B

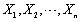 ,
,