概率论与数理统计(经管类)2013年4月真题
-
设随机变量X与Y相互独立,X~N(0,3),Y~N(1,4)。记Z=2X+Y,
求:(1)E(Z),D(Z); (2)E(XZ); (3)
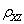 。
。 -
某次考试成绩服从正态分布N(75,152)(单位:分)。
(1)求此次考试的及格率P{X≥60}和优秀率P{X≥90};
(2)考试成绩至少高于多少分能排名前50%? (附:Φ(1)=0.8413)
-
设二维随机变量(X,Y)的概率密度为
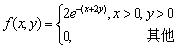
求:(1)(X,Y)关于X,Y的边缘概率密度;
(2)记Z=2X+1,求Z的概率密度。
-
某种零件直径X~N(12,σ2)(单位:mm),σ2未知。现用一种新工艺生产此种零件,随机取出16个零件,测其直径,算得样本均值,样本标准差s=0.8,问用新工艺生产的零件平均直径与以往是否有显著变化?(α=0.05)(附:
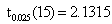 )
) -
在一元线性回归模型中
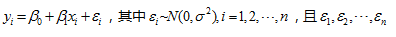 相互独立。令
相互独立。令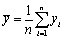 ,则
,则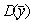 =________。
=________。 -
甲、乙两人从装有6个白球4个黑球的盒中取球,甲先从中任取一个球,不放回,而后乙再从盒中任取两个球。求:
(1)甲取到黑球的概率;
(2)乙取到的都是黑球的概率。
-
设
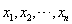 为来自总体N(μ,σ2)的样本,s2是样本方差。检验假设
为来自总体N(μ,σ2)的样本,s2是样本方差。检验假设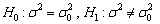 ,选取检验统计量
,选取检验统计量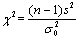 ,当H0成立时,则χ2~________。
,当H0成立时,则χ2~________。 -
设总体X服从参数是λ的指数分布,
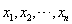 为来自该总体的样本,在对λ进行极大似然估计时,记
为来自该总体的样本,在对λ进行极大似然估计时,记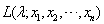 为似然函数,则当
为似然函数,则当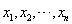 都大于0时,
都大于0时,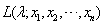 =________。
=________。 -
设总体X服从参数是λ的泊松分布,λ为未知参数,
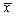 是样本均值,则λ的矩估计
是样本均值,则λ的矩估计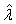 =________。
=________。 -
设总体X~N(0,4),且x1、x2、x3为来自总体X的样本,若
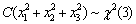 则常数C=________。
则常数C=________。 -
设
 为来自总体X的样本,且D(X)=σ2,
为来自总体X的样本,且D(X)=σ2,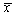 是样本均值,则
是样本均值,则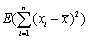 =________。
=________。 -
设随机变量X服从参数为1的指数分布,则
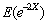 =________。
=________。 -
设随机变量X~B(100,0.5),则由切比雪夫不等式估计概率P{40
-
设C为常数,则C的方差D(C)=________。
-
设随机变量X的概率密度为
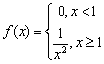 ,用Y表示对X的3次独立重复观察中事件{X>3}出现的次数,则P{Y=3}=________。
,用Y表示对X的3次独立重复观察中事件{X>3}出现的次数,则P{Y=3}=________。 -
设二维随机变量(X,Y)服从圆域D:x2+y2≤1上的均匀分布,f(x,y)为其概率密度,则f(0,0)=________。
-
设随机事件A与B相互独立,且P(A|B)=0.2,则
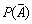 =________。
=________。 -
设随机变量X服从参数为1的泊松分布,则P{X≥1}=________。
-
从0,1,2,3,4五个数字中不放回地取3次数,每次任取一个,则第3次取到0的概率为________。
-
设总体X~N(μ,σ2),参数μ未知,σ2已知,来自总体X的一个样本的容量为n,
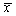 和s2分别是样本均值和样本方差,0<α<1,则μ的置信度为1-α的置信区间是()
和s2分别是样本均值和样本方差,0<α<1,则μ的置信度为1-α的置信区间是()- A.
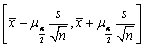
- B.
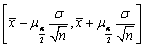
- C.
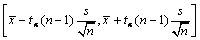
- D.
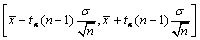
- A.
-
设A,B是随机事件,P(A)=0.4,P(B)=0.2,P(A∪B)=0.5,则P(AB)=________。
-
设是来自总体X的样本,若E(X)=μ(未知),记
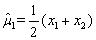 ,
,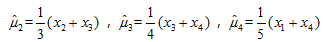 则μ的无偏估计是()
则μ的无偏估计是()- A.
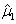
- B.
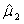
- C.
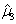
- D.
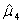
- A.
-
设随机变量X的分布函数为
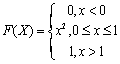 ,则E(X)=()
,则E(X)=()- A.
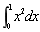
- B.
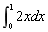
- C.
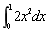
- D.
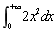
- A.
-
设总体X服从区间[θ,4θ]上的均匀分布(θ>0),
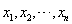 为来自X的样本,
为来自X的样本,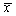 为样本均值,则
为样本均值,则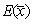 =()
=()- A.5θ
- B.3θ
- C.5θ/2
- D.3θ/2
-
设随机变量X的分布律为
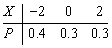 ,则E(X)=()
,则E(X)=()- A.-0.8
- B.-0.2
- C.0
- D.0.4
-
设二维随机变量(X,Y)的分布律为

则P{X=0}=()
- A.0
- B.0.1
- C.0.2
- D.0.3
-
设二维随机变量(X,Y)的概率密度为
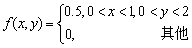 ,则P{X≤0.5,Y≤1}=()
,则P{X≤0.5,Y≤1}=()- A.0.25
- B.0.5
- C.0.75
- D.1
-
设随机变量X的分布函数为F(x),则P{a
- A.F(b-0)-F(a-0)
- B.F(b-0)-F(a)
- C.F(b)-F(a-0)
- D.F(b)-F(a)
-
设A、B为随机事件,
 ,P(AB)=0.2,则P(A-B)=()
,P(AB)=0.2,则P(A-B)=()- A.0.1
- B.0.2
- C.0.3
- D.0.4
-
甲、乙两人向同一目标射击,A表示“甲命中目标”,B表示“乙命中目标”,C表示“命中目标”,则C=()
- A.A
- B.B
- C.AB
- D.A∪B
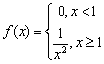 ,用Y表示对X的3次独立重复观察中事件{X>3}出现的次数,则P{Y=3}=________。
,用Y表示对X的3次独立重复观察中事件{X>3}出现的次数,则P{Y=3}=________。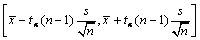
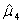
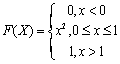 ,则E(X)=()
,则E(X)=()