概率论与数理统计(经管类)2011年7月真题
-
设二维随机变量(X,Y)的联合分布为
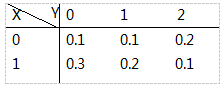
求
 。
。 -
已知某果园每株梨树的产量X(单位:kg)服从正态分布N(240,σ2),今年雨量有些偏少,在收获季节从果园一片梨树中随机抽取6株,测算其平均产量为220kg,产量方差为662.4kg,试在检验水平α=0.05下,检验:
(1)今年果园每株梨树的平均产量μ的取值为240kg能否成立?
(2)若设X~N(240,200),能否认为今年果园每株梨树的产量的方差σ2有显著变化?
(
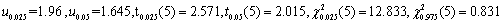 )
) -
设随机变量X、Y在区域D{(X,Y):0
-
设二维随机变量(X,Y)的概率密度为
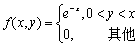
(1)分别求(X,Y)关于X和Y的边缘概率密度
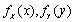 ;
;(2)判断X与Y是否相互独立,并说明理由;
(3)计算P{X+Y≤1}。
-
设α,β分别是假设检验中犯第一、二类错误的概率,H0,H1分别为原假设和备择假设,则P{拒绝H0|H0不真}=________。
-
已知一元线性回归方程为
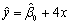 ,且
,且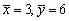 ,则
,则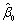 =________。
=________。 -
设P(A)=0.4,P(B)=0.5,且
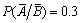 ,求P(AB)。
,求P(AB)。 -
设随机变量X~N(0,1),Y~χ2(n),且X,Y相互独立,则
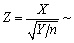 ________。
________。 -
由来自正态总体X~N(μ,0.99)、容量为15的简单随机样本,得样本均值为2.88,则μ的置信度为0.95的置信区间是________。(
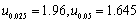 )
) -
设二维随机变量(X,Y)的概率密度为
 ,则(X,Y)的分布函数为________。
,则(X,Y)的分布函数为________。 -
设随机变量X的数学期望E(X)与方差D(X)都存在,且有E(X)=10,E(X2)=109,试由切比雪夫不等式估计
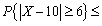 ________。
________。 -
设随机变量X,Y相互独立,且有如下分布:

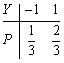
则E(XY)=________。
-
设二维离散型随机变量(X,Y)的联合分布律为
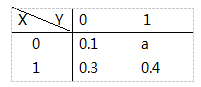 ,
,则a=________。
-
设二维随机变量(X,Y)服从区域G:0≤x≤2,0≤y≤2上的均匀分布,则P{X≤1,Y≤1}=________。
-
设随机变量X的分布律为
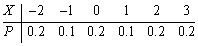 ,记Y=X2,则P{Y≥4}=________。
,记Y=X2,则P{Y≥4}=________。 -
设随机变量X~P(λ),且P{X=0}=e-1,则P{X=k}(k=1,2,…)=________。
-
设连续型随机变量X的分布函数为
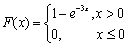 ,则P{X≤1}=________。
,则P{X≤1}=________。 -
设A、B为随机事件,且P(A)=0.8,P(B)=0.4,P(B|A)=0.25,则P(A|B)=________。
-
某射手命中率为2/3,他独立地向目标射击4次,则至少命中1次的概率为________。
-
对非正态总体X,当样本容量n≥50时,对总体均值进行假设检验就可采用()
- A.u检验
- B.t检验
- C.χ2检验
- D.F检验
-
100件产品中有10件次品,不放回地从中接连取两次,每次取一个产品,则第二次取到次品的概率为________。
-
设总体X~N(0,1),来自X的
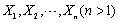 一个样本,
一个样本,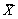 、S分别是样本均值与样本方差,则有()
、S分别是样本均值与样本方差,则有()- A.
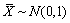
- B.
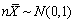
- C.
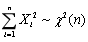
- D.
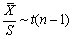
- A.
-
设随机变量X~N(0,1),Y~N(0,1),令Z=X+Y,则有()
- A.E(Z)=0
- B.E(Z)=2
- C.D(Z)=1
- D.D(Z)=2
-
设X1、X2来自任意总体X的一个容量为2的样本,则在下列E(X)的无偏估计量中,最有效地估计量是()
- A.
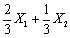
- B.
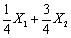
- C.
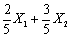
- D.
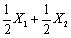
- A.
-
设二维随机变量(X,Y)的联合分布律为
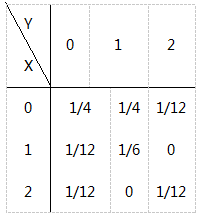
则P{X=0}=()
- A.1/4
- B.1/3
- C.5/12
- D.7/12
-
已知二维随机变量(X,Y)的概率密度为
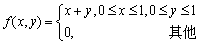 ,P{X
,P{X- A.1/3
- B.2/3
- C.1/2
- D.1/4
-
设随机变量X~N(1,22),Φ(1)=0.8413,则P{1≤X≤3}=()
- A.0.1385
- B.0.2413
- C.0.2934
- D.0.3413
-
设随机变量X的分布律为
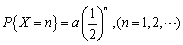 ,则a=()
,则a=()- A.1
- B.1/2
- C.2
- D.3
-
对于任意两事件A、B,P(A-B)=()
- A.P(A)-P(B)
- B.P(A)-P(B)+P(AB)
- C.P(A)-P(AB)
- D.
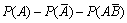
-
设A、B为随机事件,且
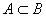 ,则
,则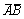 =()
=()- A.
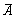
- B.
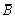
- C.

- D.
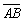
- A.


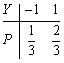
 ,
,