概率论与数理统计(经管类)2011年4月真题
-
设二维随机变量(X,Y)的分布律为
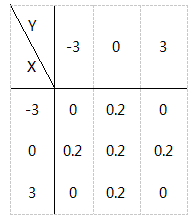
求:
(1)(X,Y)分别关于X,Y的边缘分布律;
(2)D(X),D(Y),Cov(X,Y)。
-
某种装置中有两个相互独立工作的电子元件,其中一个电子元件的使用寿命X(单位:小时)服从参数1/1000的指数分布,另一个电子元件的使用寿命Y(单位:小时)服从参数1/2000的指数分布。试求:
(1)(X,Y)的概率密度;
(2)E(X),E(Y);
(3)两个电子元件的使用寿命均大于1200小时的概率。
-
设随机变量X的概率密度为,且
 P{X≥1}=1/4。
P{X≥1}=1/4。求:
(1)常数a,b;
(2)X的分布函数F(X);
(3)E(X)。
-
设总体X的概率密度为
 ,其中未知参数θ>0,
,其中未知参数θ>0,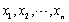 为来自总体X的一个样本。求θ的极大似然估计
为来自总体X的一个样本。求θ的极大似然估计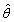 。
。 -
盒中有3个新球、1个旧球,第一次使用时从中随机取一个,用后放回,第二次使用时从中随机取两个,事件A表示“第二次取到的全是新球”,求P(A)。
-
设总体X~N(μ,σ2),σ2已知,
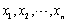 为来自总体X的一个样本,
为来自总体X的一个样本,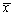 为样本均值,则参数μ的置信度为1-α的置信区间为________。
为样本均值,则参数μ的置信度为1-α的置信区间为________。 -
设总体X~N(μ,4),x1,x2,…,x16为来自总体X的一个样本,
 为样本均值,则检验假设
为样本均值,则检验假设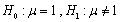 ,应采用的检验统计量的表达式为________。
,应采用的检验统计量的表达式为________。 -
设总体X~N(μ,σ2),
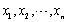 为来自总体X的一个样本,
为来自总体X的一个样本,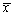 为样本均值,s2为样本方差,则
为样本均值,s2为样本方差,则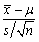 ~________。
~________。 -
设总体X的概率密度为f(x;θ),其中θ为未知参数,且E(X)=2θ,
 为来自总体X的一个样本,
为来自总体X的一个样本,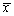 为样本均值。若
为样本均值。若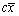 为θ的无偏估计,则常数c=________。
为θ的无偏估计,则常数c=________。 -
设随机变量
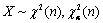 是自由度为n的χ2分布的α分位数,则
是自由度为n的χ2分布的α分位数,则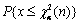 =________。
=________。 -
设总体X~N(μ,64),x1,x2,…,x8为来自总体X的一个样本,
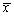 为样本均值,则
为样本均值,则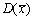 =________。
=________。 -
设随机变量X1,X2,…,Xn,…相互独立同分布,且
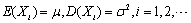 ,则
,则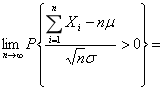 ________。
________。 -
设随机变量X与Y相互独立,X在区间[0,3]上服从均匀分布,Y服从参数为4的指数分布,则D(X+Y)=________。
-
设X为随机变量,E(X+3)=5,D(2X)=4,则E(X2)=________。
-
设二维随机变量(X,Y)的分布律为
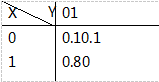 则P{X=0,Y=1}=________。
则P{X=0,Y=1}=________。 -
设随机变量X~N(0,42),且P{X>1}=0.4013,Φ(x)为标准正态分布函数,则Φ(0.25)=________。
-
设二维随机变量(X,Y)的概率密度为
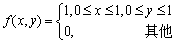 ,则P{X+Y>1}=________。
,则P{X+Y>1}=________。 -
设随机变量X服从参数为3的泊松分布,则P{X=2}=________。
-
设随机事件A与B互不相容,P(
 )=0.6,P(A∪B)=0.8,则P(B)=________。
)=0.6,P(A∪B)=0.8,则P(B)=________。 -
设随机变量X~χ2(2),Y~χ2(3),且X与Y相互独立,则
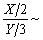 ()
()- A.χ2(5)
- B.t(5)
- C.F(2,3)
- D.F(3,2)
-
设A,B为随机事件,P(A)=0.6,P(B|A)=0.3,则P(AB)=________。
-
在假设检验中,H0为原假设,则显著性水平
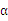 的意义是()
的意义是()- A.P{拒绝H0|H0为真}
- B.P{接受H0|H0为真}
- C.P{接受H0|H0不真}
- D.P{拒绝H0|H0不真}
-
设随机变量X~N(-1,22),Y~N(-2,32),且X与Y相互独立,则X-Y~()
- A.N(-3,-5)
- B.N(-3,13)
- C.N(1,
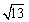 )
) - D.N(1,13)
-
设X,Y为随机变量,D(X)=4,D(Y)=16,Cov(X,Y)=2,则
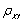 =()
=()- A.1/32
- B.1/16
- C.1/8
- D.1/4
-
设随机变量X的概率密度为
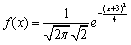 ,则E(X),D(X)分别为()
,则E(X),D(X)分别为()- A.-3,
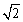
- B.-3,2
- C.3,
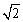
- D.3,2
- A.-3,
-
已知随机变量X的分布律为
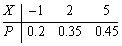 ,则P{-2
,则P{-2- A.0.2
- B.0.35
- C.0.55
- D.0.8
-
设二维随机变量(X,Y)的概率密度为
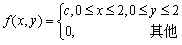 ,则常数c=()
,则常数c=()- A.1/4
- B.1/2
- C.2
- D.4
-
设随机事件A与B相互独立,且P(A)=1/5,P(B)=3/5,则P(A∪B)=()
- A.3/25
- B.17/25
- C.4/5
- D.23/25
-
设随机变量X~B(3,0.4),则P{X≥1}=()
- A.0.352
- B.0.432
- C.0.784
- D.0.936
-
设A,B,C为随机事件,则事件“A,B,C都不发生”可表示为()
- A.
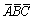
- B.
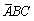
- C.ABC
- D.

- A.

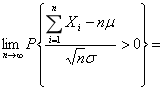 ________。
________。 则P{X=0,Y=1}=________。
则P{X=0,Y=1}=________。 )
)