2015年成人高考高起点数学(文史财经类)真题及答案
-
(Ⅱ)若E的焦距为2,求其方程
-
(本小题满分13分)
设椭圆
 的左、右焦点分别为F1??和F2??,直线l过且斜率为3/4,A(x0??,y0?)(y>0)为l和E的交点,AF2??丄F1?F2????????
的左、右焦点分别为F1??和F2??,直线l过且斜率为3/4,A(x0??,y0?)(y>0)为l和E的交点,AF2??丄F1?F2????????(I)求E的离心率;
-
(Ⅱ)f(x)的单调区间,并指出f(x)在各个单调区间的单调性
-
(Ⅱ)若{an}的前n项和Sn=50,求n
-
已知函数f(x)=x3??+ax2??+b在x=1处取得极值-1,求(I)a,b;????
-
已知△ABC中,A= 30°,AC=BC=1.求(I)AB;
-
(Ⅱ)△ABC的面积.
-
已知等差数列的公差d≠0,a1=1/2,且a1,a2,a5成等比数列.
(I)求{an}的通项公式;
-
曲线:y=x2??+3x+4在点(-1,2)处的切线方程为
-
从某公司生产的安全带中随机抽取10条进行断力测试,测试结果(单位:kg)如下:
3722 3872 4004 4012 3972 3778 4022 4006 3986 4026
则该样本的样本方差为kg2(精确到0.1)
-
设f(x)为偶函数,若f(-2)=3,则f(2)=
- A.6
- B.-3
- C.0
- D.3
-
拋物线y2??= 2px的准线过双曲线x2??/3-y2??= 1的左焦点,则p=??
-
不等式 |x -1|<1的解集为
-
以点(0,1)为圆心且与直线
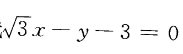 相切的圆的方程为
相切的圆的方程为- A.(x—1)2+y2??=1??
- B.x2+ (y— l)2= 2
- C.x2+( y—l)2=4
- D.x2+ (y—l)2=16
-
某学校为新生开设了4门选修课程,规定每位新生至少要选其中3门,则一位新生不同的选课方案共有 ( )
- A.7种
- B.4种
- C.5种
- D.6种
-
设tanθ=2,则tan(θ+π)
- A.-2
- B.2
- C.1
- D.-1/2
-
下列不等式成立的是

- A.A
- B.B
- C.C
- D.D
-
已知点A(1,1),B(2,1),C(-2,3),则过点A及线段BC中点的直线方程为 ( )
- A.x-y+2=0
- B.x+y-2=0
- C.x+y+2=0
- D.x-y=0
-
log510 — log5??2=????
- A.8
- B.0
- C.1
- D.5
-
设二次函数y=ax2+bx+c的图像过点(-1,2)和(3,2),则其对称轴的方程为( )
- A.x=-1
- B.x=3
- C.x=2
- D.x=1
-
设甲:函数y=kx+b的图像过点(1,1),
乙:k+6=1,则 ( )
- A.A.甲是乙的充分必要条件
- B.B.甲是乙的必要条件,但不是乙的充分条件
- C.C.甲是乙的充分条件,但不是乙的必要条件
- D.D.甲不是乙的充分条件,也不是乙的必要条件
-
下列函数在各自定义域中为增函数的是
- A.y=1+2x
- B.y=1—x
- C.y=1+x2
- D.y=1+Z-x
-
若等比数列{an}的公比为3,a4=??9,则a1=??
- A.27
- B.1/9
- C.1/3
- D.3
-
设函数
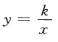 的图像经过点(2,-2),则k=
的图像经过点(2,-2),则k=- A.A.-4
- B.B.4
- C.C.1
- D.D.-1
-
设集合M={2,5,8},N={6,8},则以MUN
- A.{2,5,6}
- B.{8}
- C.{6}
- D.{2,5,6,8}
-
函数:
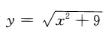 的值域为
的值域为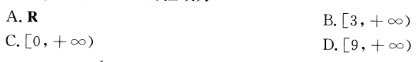
- A.A
- B.B
- C.C
- D.D
-
若
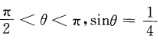 则
则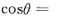

- A.A
- B.B
- C.C
- D.D
-
已知平面向量(-2,1)与b= (A,2)垂直,则A=
- A.4
- B.-4
- C.-1
- D.1
-
甲、乙两人独立地破译一个密码,设两人能破译的概率分别为p1,p2,则恰有一人能破译的概率为 ( )

- A.A
- B.B
- C.C
- D.D
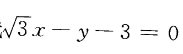 相切的圆的方程为
相切的圆的方程为