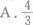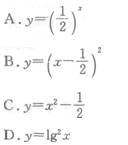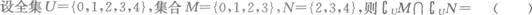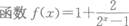2012年成人高考《数学(理工农医类)高起点》最后冲刺试卷(五)
-
设函数f(x)=3x5-5x3,求
(Ⅰ)f(x)的单调区间;
(Ⅱ)f(x)的极值.
-

-

(Ⅰ)双曲线的标准方程;(Ⅱ)双曲线的焦点坐标和准线方程.
-

(Ⅰ)f(x)的单调区间,并判断它在各单调区间上是增函数还是减函数;
(Ⅱ)f(x)在[-2,0]上的最大值与最小值.
-

-

-

-

-
使函数y=x2-2x-3为增函数的区间是( )
- A.(1,+∞)
- B.(-∞,3)
- C.(3,+∞)
- D.(-∞.1)
-
已知空间中两条直线m,n,且m在平面α内,n在平面β内,设甲:m//β,n//α;乙:平面α//平面β,则( )
- A.甲为乙的必要但非充分条件
- B.甲为乙的充分但非必要条件
- C.甲非乙的充分也非必要条件
- D.甲为乙的充分必要条件
-
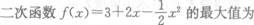
- A.2
- B.3
- C.4
- D.5
-
若f(x+1)=x2-2x+3,则f(x)=( )
- A.x2+2x+6
- B.x2+4x+6
- C.x2-2x+6
- D.x2-4x+6
-
在点x=0处的导数等于零的函数是( )
- A.y=sinx
- B.y=x-1
- C.y=ex-x
- D.y=x2-x
-
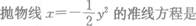
- A.x=1
- B.y=1
- C.x=-1
- D.y=-1
-
若函数
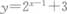 的反函数的图像经过点P,则点P的坐标是( )
的反函数的图像经过点P,则点P的坐标是( )- A.(1,2)
- B.(2,1)
- C.(2,5)
- D.(5,2)
-
函数f(x)=2x-1的反函数的定义域是( )
- A.(1,+∞)
- B.(-1,+∞)
- C.(0。+∞)
- D.(-∞,+∞)
-
已知空间向量a=(6,-4,2),b=(x,2,3),且a⊥b,则x=
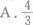
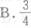
C.3
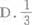
-
设函数f(x)=ex,则.f(x-a)·f(x+a)=( )
- A.f(x2-a2)
- B.2f(x)
- C.f(x2)
- D.f2(x)
-
抛物线y2=4x上一点P到焦点F的距离是10,则点P坐标是( )
- A.(9,6)
- B.(9,±6)
- C.(6,9)
- D.(±6,9)
-
下列函数中,为偶函数的是
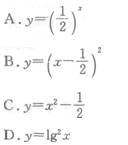
-

- A.4
- B.2
- C.1
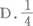
-

- A.为奇函数且在(-∞,0)上是减函数
- B.为奇函数且在(-∞,0)上是增函数
- C.为偶函数且在(0,+∞)上是减函数
- D.为偶函数且在(0,+∞)上是增函数
-
函数y=lg(x2-3x+2)的定义域为( )
- A.{x|x<1或x>2}
- B.{x|1<x<2}
- C.{x|x<1}
- D.{x|x>2}
-
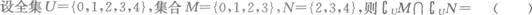
- A.{2,3)
- B.{0,1,4}
- C.φ
- D.U
-
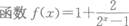
- A.是奇函数
- B.是偶函数
- C.既是奇函数,又是偶函数
- D.既不是奇函数,又不是偶函数







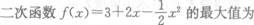
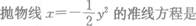
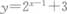 的反函数的图像经过点P,则点P的坐标是( )
的反函数的图像经过点P,则点P的坐标是( )