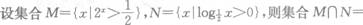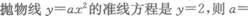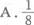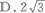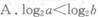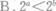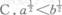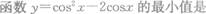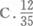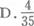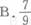2012年成人高考《数学(理工农医类)高起点》最后冲刺试卷(三)
-

-

-
函数f(x)=ax3+bx2+cx+d,当x=-1时,取得极大值8,当x=2时,取得极大值-19.
(Ⅰ)求y=f(x);
(Ⅱ)求曲线y=f(x)在点(-1,8)处的切线方程.
-
设A,B为二次函数y=-3x2-2x+a的图象与x轴的两个不同的交点,点P为抛物线的顶点,当△PAB为等腰直角三角形时,求a的值.
-
已知球的球面积为16n,则此球的体积为_________.
-
球的体积与其内接正方体的体积之比为_________.
-

-

-
已知平面向量a={3,x),b=-(-2,5),且a⊥b,则2=( )

-



C.2
D.-2
-
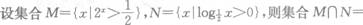
- A.{x|0<x<1}
- B.{x|-1<x<1}
- C.{x|0<x<2}
- D.{x|x>1}
-
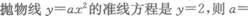
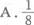

C.8
D.-8
-

- A.8
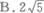
- C.4
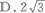
- A.8
-
若函数f(x)=log2(5x+1),则其反函数y=f-1(x)的图像过点( )
- A.(2,1)
- B.(3,2)
- C.(2,3)
- D.(4,3)
-
若a>b>0,则( )
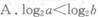
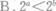
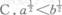
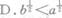
-
过M(3,2),且与向量a=(-4,2)垂直的直线方程为( )
- A.2x+y-4=0
- B.2x-y+4=0
- C.2x-y-4=0
- D.2x+y+4=0
-
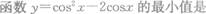
- A.2
- B.1
- C.0
- D.-1
-
盒中有3个红球和4个白球,从中随机抽取3球,其中最多有一个白球的概率是( )
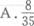
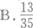
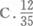
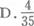
-
圆x2+y2=25上的点到直线5x+12y-169=0的距离的最小值是( )
- A.9
- B.8
- C.7
- D.6
-

- A.(-∞,03∪[2,+∞)
- B.[0,2]
- C.(-∞,0)∏∪2,+∞)
- D.(0,2)
-
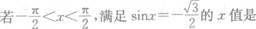
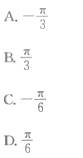
-
函数y=log3(x+1)的反函数为
- A.
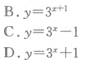
- A.
-

- A.1
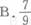

- A.1
-
下列关系式中,对任意实数A<B<0都成立的是( )
- A.a2<b2
- B.1g(b-a)>0
- C.2a<2b
- D.lg(-a)<lg(-b)
-
函数F(x)=f(x)·sinx是奇函数,则f(x)( )
- A.是偶函数
- B.是奇函数
- C.既是偶函数又是奇函数
- D.既不是偶函数又不是奇函数