2014年成人高考高升本《数学理工类》考前密押试卷（2）

如果您发现本试卷没有包含本套题的全部小题，请尝试在页面顶部本站内搜索框搜索相关题目，一般都能找到。

已知数列{an}的前n项和Sn=nbn，其中{bn}是首项为1，公差为2的等差数列．（I）求数列{an}的通项公式；
点击查看答案
(I)求此双曲线的渐近线ι1，ι2的方程；
(Ⅱ)设A，B分别为ι1，ι2上的动点，且2|AB|=5|F1F2|，求线段AB中点M的轨迹方程．并说明是什么曲线．
点击查看答案
已知函数?（x）=（x2+ax+2）ex（x，a∈R）．（I）当a=0时，求函数?（x）的图象在点A（1，?（1））处的切线方程；（Ⅱ）当a=-5/2时，求函数?（x）的极小值．
点击查看答案
设i，j，k为单位向量且互相垂直，向量a=i+j，b=-i+j-k，则a·b= __________.
点击查看答案
(Ⅰ)求△ABC的最小角的大小；
(Ⅱ)求／kABC的面积
点击查看答案
正方体ABCD—A ˊBˊCˊD ˊ中，A ˊC ˊ与B ˊC所成的角为__________．
点击查看答案
已知双曲线的离心率是2，则两条渐近线的夹角是__________．
点击查看答案
- A.A
- B.B
- C.C
- D.D
点击查看答案
海上有A，B两个小岛相距10海里，从A岛望C岛和B岛成60o的视角，从B岛望C岛和A岛成75o的视角，则B，C之间的距离是__________．
点击查看答案
不等式| x-2|≤7的解集是（　　）
- A.{x|x≤9}
- B.{x|x≥一5}
- C.{x|x≤-5或x≥9}
- D.{x|-5≤x≤9}
点击查看答案
平面上到两定点F1（-7，0），F2（7，0）距离之差的绝对值等于10的点的轨迹方程为（　　）
点击查看答案
- A.8/25
- B.9/25
- C.12/25
- D.24/25
点击查看答案
- A.8
- B.6
- C.C
- D.D
点击查看答案
已知m，n是不同的直线，a，β是不同的平面，且m⊥a，
- A.若a∥β，则m⊥n
- B.若a⊥β，则m∥n
- C.若m⊥n，则a∥β
- D.若n∥a，则β∥a
点击查看答案
B.
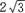
- A.2
- B.B
- C.3
- D.4
点击查看答案
已知正三棱锥S—ABC的三个侧面均为等腰直角三角形，且底面边长为压，则此棱锥的体积为（　　）
- A.A
- B.B
- C.C
- D.D
点击查看答案
若-1，以，6，c，-9五个数成等比数列，则
- A.b=3，ac=9
- B.b=－3，ac=9
- C.b=－3，ac=－9
- D.b=3，ac=－9
点击查看答案
log7[log3(log2x)]=0，那么x1/2的值是（　　）
- A.A
- B.B
- C.C
- D.D
点击查看答案
设Sn=（3-1）+（32-2）+（33-3）+…+（3n-n），那么S10的值等于（　　）
- A.A
- B.B
- C.C
- D.D
点击查看答案
设命题甲：k=1，命题乙：直线y=kx与直线y=x+1平行，则（　　）
- A.甲是乙的必要条件但不是乙的充分条件
- B.甲是乙的充分条件但不是乙的必要条件
- C.甲既不是乙的充分条件也不是乙的必要条件
- D.甲是乙的充分必要条件
点击查看答案
已知直线ι1，ι2的斜率是方程6x2+x-1=0的两个根，那么ι1与ι2所成的角是（　　）
- A.15o
- B.30o
- C.45o
- D.60o
点击查看答案
两个盒子内各有3个同样的小球，每个盒子中的小球上分别标有1，2，3三个数字．从两个盒子中分别任意取出一个球，则取出的两个球上所标数字的和为3的概率是（　　）
点击查看答案
一个圆柱的轴截面面积为Q，那么它的侧面积是（　　）
- A.1/2πQ
- B.πQ
- C.2πQ
- D.以上都不对
点击查看答案
2
在长方体ABCD—A1B1C1D1中，B1C和C1D与底面所成的角分别为60o和45o，则异面直线B1C和C1D所成的角的余弦值为（　　）
- A.A
- B.B
- C.C
- D.D
点击查看答案
一个科研小组共有8名科研人员，其中有3名女性．从中选出3人参加学术讨论会，选出的人必须有男有女，则有不同选法（　　）
- A.56种
- B.45种
- C.10种
- D.6种
点击查看答案