2017年成人高考高升本数学《理工农医类》真题

已知关于x,y 的方程

证明：

(1)无论θ为何值，方程均表示半径为定长的圆;

(2)当θ=π/4时，判断该圆与直线：y =x的位置关系.

设直线y=x + 1是曲线的切线，求切点坐标和a的值.

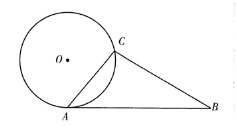
如图，AB与半径为1的〇O相切于A点，AE = 3，AB与〇O的弦AC的夹角为50°.求

(1)AC；

(2) △

ABC的面积.（精确到0. 01)

若5条鱼的平均质量为0.8kg，其中3条的质量分别为0.75kg，0.83kg和0.78kg，则其余2条的平均质量为________kg.

已知平面向量a=(l，2)，b=(―2,3)，2a+3b=________.

已知直线l和x—y+1=0关于直线x=-2对称，则l的斜率为________.

若1名女生和3名男生随机地站成一列，则从前面数第2名是女生的概率为（）。

• A.A
• B.B
• C.C
• D.D

  （）。

• A.100
• B.40
• C.10
• D.20

双曲线的焦距为（）。

• A.1
• B.4
• C.2
• D.    

已知三角形的两个顶点是椭圆的两个焦点，第三个顶点在C上，则该三角形的周长为（）。

• A.10
• B.20
• C.16
• D.26

函数的图像与直线x+3 = 0的交点坐标为（）。

• A.A
• B.B
• C.C
• D.D

若 lg5 = m，则lg2=（）。

• A.5m
• B.1 - m
• C.2m
• D.m + 1

设f (x+1) = x(x+1)，则 f(2)=（）。

• A.1
• B.3
• C.2
• D.6

—个圆上有5个不同的点，以这5个点中任意3个为顶点的三角形共有（）。

• A.60 个
• B.15 个
• C.5 个
• D.10 个

 （）。

• A.奇函数，且在（0, +∞)单调递增
• B.偶函数，且在(0，+∞)单调递减
• C.奇函数，且在(-∞，0)单调递减
• D.偶函数，且在(-∞，0)单调递增

已知点义(4，1)，5(2,3)，则线段八5的垂直平分线方程为（）。

• A.x - y + 1 = 0
• B.x + y - 5 = 0
• C.x - y -1 = 0
• D.x - 2y + 1 = 0

函数y = 6sinxcosx的最大值为（）。

• A.1
• B.2
• C.6
• D.3

右图是二次函数 的部分图像，则（）。

• A.b >0，c >0
• B.b >0，c< 0
• C.b<0，c>0
• D.b<0，c<0

（）。

• A.A
• B.B
• C.C
• D.D

设a，b，c为实数，则（）。

• A.a - c>b –c
• B.|a|＞|b|
• C.
• D.ac＞bc

函数的定义域为（）。

• A.{ x | x≥0}
• B.{ x | x≥1}
• C.{x| 0≤x ≤1}
• D.{x|x≤0 或x≥1}

设集合 M ={1,2,3,4,5}，N = {2,4,6}，则 M∩N =（）。

• A.{2,4}
• B.{2,4,6}
• C.{1,3,5}
• D.{1，2,3,4,5,6}

函数的最小正周期是（）。

• A.8π
• B.4π
• C.2π
• D.