重庆市第79中学2012届九年级上学期期中考试数学试题
-
在直角坐标平面内,O为原点,点A的坐标为(1,0),点C的坐标为(0,4),直线CM∥
 轴(如图所示).点B与点A关于原点对称,直线y=x+b(
轴(如图所示).点B与点A关于原点对称,直线y=x+b( 为常数)经过点B,且与直线CM相交于点D,连结 OD.
为常数)经过点B,且与直线CM相交于点D,连结 OD.(1)求b的值和点D的坐标;
(2)设点P在
 轴的正半轴上,若△POD是等腰三角形,求点P的坐标;
轴的正半轴上,若△POD是等腰三角形,求点P的坐标;(3)在(2)的条件下,如果以PD为半径的圆P与圆O外切,求圆O的半径.

-
如图,在平面直角坐标系中,⊙M与x轴交于A、B两点,AC是⊙M的直径,过点C的直线交x轴于点D,连接BC,已知点M的坐标为(0,
 ),直线CD的函数解析式为y=-
),直线CD的函数解析式为y=- x+5
x+5 .
.⑴求点D的坐标和BC的长;
⑵求点C的坐标和⊙M的半径;
⑶求证:CD是⊙M的切线.

-
随着人们经济收入的不断提高及汽车产业的快速发展,汽车已越来越多地进入普通家庭,成为居民消费新的增长点.据某市交通部门统计,2007年底全市汽车拥有量为180万辆,而截止到2009年底,全市的汽车拥有量已达216万辆.
(1)求2007年底至2009年底该市汽车拥有量的年平均增长率;
(2)为保护城市环境,缓解汽车拥堵状况,该市交通部门拟控制汽车总量,要求到2011年底全市汽车拥有量不超过231.96万辆;另据估计,从2010年初起,该市此后每年报废的汽车数量是上年底汽车拥有量的10%.假定每年新增汽车数量相同,请你计算出该市每年新增汽车数量最多不能超过多少万辆.
(提示:
 )
) -
已知:关于x的方程2x2+kx-1=0
(1)求证:方程有两个不相等的实数根;
(2)若方程的一个根是-1,求另一个根及k值
-
如图,矩形ABCD的长AB=4cm.宽BC=3cm,P、Q以1cm/s的速度分别从A、B出发,沿AB、BC方向前进,经多少秒后P、Q之间的距离为 2
 cm?
cm?
-
先化简,再求值:
 其中
其中 .
. -
如图9所示,每个小方格都是边长为1的正方形,以O点为坐标原点建立平面直角坐标系.
(1)画出四边形OABC关于y轴对称的四边形OA1B1C1,并写出点B1的坐标是 .
(2)画出四边形OABC绕点O顺时针方向旋转90°后得到的四边形OA2B2C2.

-
已知:如图△ABC内接于⊙O,OH⊥AC于H,过A点的切线与OC的延长线交于点D,∠B=30°,OH=5
 .请求出:
.请求出:(1)∠AOC的度数;
(2)劣弧AC的长(结果保留π);
(3)线段AD的长(结果保留根号).

-

-

-

-

-
如图,已知A、B两点的坐标分别为(2,0)、(0,2),⊙C的圆心坐标为(-1,0),半径为1.若D是⊙C上的一个动点,线段DA与y轴交于点E,则△ABE面积的最小值是_____________

-
如图,在直角坐标系中,已知点A(-3,0),B(0,4), 对
 连续作旋转变换,依次得带三角形 ①,②,③,④,…,三角形⑩的直角顶点的坐标为__________
连续作旋转变换,依次得带三角形 ①,②,③,④,…,三角形⑩的直角顶点的坐标为__________
-
如图,四边形OABC为菱形,点B、C在以点O为圆心的
 上,若
上,若 ,
,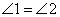 ,则弧
,则弧 的长为 cm.
的长为 cm.
-
已知关于x的一元二次方程
 的一个根是0,则a=______
的一个根是0,则a=______ -
方程(x-2)(x-3)=0的解是_________
-
若最简二次根式
 与
与 是同类二次根式,则a的值为_________
是同类二次根式,则a的值为_________ -
如图⊙O的弦AB⊥CD于H,D、E关于AB对称,BE延长线交⊙O于F,连接FC,作OG⊥AB于G,
则下列结论: ①FC=CE, ②
 弧AF=弧AD ,③ OG=
弧AF=弧AD ,③ OG= CF,④GH=BH成立的是( )
CF,④GH=BH成立的是( )- A、①②③ B、①②④ C、②③④ D、①②③④

- A、①②③ B、①②④ C、②③④ D、①②③④
-
等式
 成立的条件是(
成立的条件是( )
)- A. x≥1 B. x≥-1 C. -1
 ≤x≤1 D. x≤1或x≥-1
≤x≤1 D. x≤1或x≥-1
- A. x≥1 B. x≥-1 C. -1
-
如图,边长为1的正方形ABCD绕点A逆时针旋转
 到正方形
到正方形 ,图中阴影部分的面积为
,图中阴影部分的面积为( )

-
如图,
 可以看作是由
可以看作是由 绕点O顺时针旋转α角度得到的.若点A'在AB上,则旋转角α的大小可以是( )
绕点O顺时针旋转α角度得到的.若点A'在AB上,则旋转角α的大小可以是( )- A.
 B.
B.
- A.
-
已知:如图⊙O的弦AB、CD相交于E,
 的度数为
的度数为 ,
, 的度数为
的度数为 ,则
,则 ( )
( )- A.60° B.100° C.80° D.70°

- A.60° B.100° C.80° D.70°
-
若关于x的一元二次方程
 没有实数根,则实数m的取值范围是( )
没有实数根,则实数m的取值范围是( )- A.m<1 B. m>-1 C. m>1 D.m<-1
-
用配方法解方程
 时,原方程应变形为( )
时,原方程应变形为( )- A.
 B.
B. &
&
- A.
-
二次根式
 的值是( )
的值是( )- A. -3 B. 3或-3
 C. 9 &nbs
C. 9 &nbs
- A. -3 B. 3或-3
-
下列各数中,最小的数是 ( )
- A.-1 B. -2 C.0 D.1












