高职单招数学精选试题附答案(4)
-
求过点P(2,3)且被两条直线
 :3x+4y-7=0,
:3x+4y-7=0, :3x+4y+8=0所截得的线段长为
:3x+4y+8=0所截得的线段长为 的直线方程。
的直线方程。 -
在三棱锥P-ABC中,已知PA丄BC,PA=a,EC=b,PA,BC的公垂线EF=h,求三棱锥的体积
-
四棱锥S-ABCD中,底面ABOD为平行四边形,侧面SBC丄底面ABCD
(1)证明:SA丄BC
(2)求直线SD与平面SBC所成角的正弦值。

-
设拋物线y2=4x与直线y=2x+b相交A,B于两点,弦AB长
 ,求b的值。
,求b的值。 -
计算:已知平行四边形ABCD中,A(-1,0),B(-1,-4),C(3,-2),E是AD的中点,求

-
已知函数
 ,且
,且 .
.(1)求a的值;
(2)求f(x)函数的定义域及值域.
-
已知cos=
 ,
, ,求cos
,求cos 的值.
的值. -
等差数列
 中,a2=2,a6=18,则S8=_____.
中,a2=2,a6=18,则S8=_____. -
在P(a,3)到直线4x-3y+1=0的距离是4,则a=_____.
-
 则a·b夹角为_____.
则a·b夹角为_____. -
若直线6x-4x+7=0与直线ax+2y-6=0平行,则a的值等于_____.
-
5人站成一排,甲、乙两人必须站两端的排法种数是()
- A.6
- B.12
- C.24
- D.120
-
5个人站在一其照相,甲、乙两人间恰好有一个人的排法有_____种.
-
已知一元二次不等式ax2+bx+1>0的解是
 <x<
<x<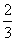 ,那么()
,那么()- A.

- B.

- C.

- D.

- A.
-
函数y=f(x)存在反函数,若f(2)=-3,则函数y=f-1(x)的图像经过点()
- A.(-3,2)
- B.(1,3)
- C.(-2,2)
- D.(-3,3)
-
若f(x)=logax(a>0且a≠1)的图像与g(x)=logbx(b>0,b≠1)的关于x轴对称,则下列正确的是()
- A.a>b
- B.a=b
- C.a<b
- D.AB=1
-
拋掷两枚骰子,两次点数之和等于5的概率是()
- A.

- B.

- C.

- D.
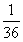
- A.
-
某品牌的电脑光驱,使用事件在12000h以上损坏的概率是0.2,则三个里最多有一个损坏的概率是()
- A.0.74
- B.0.096
- C.0.008
- D.0.512
-
二项式(x-2)7展开式中含x5的系数等于()
- A.-21
- B.21
- C.-84
- D.84
-
已知
 让点P到椭圆的一个焦点的距离为3,则它到另一个焦点的距离为()
让点P到椭圆的一个焦点的距离为3,则它到另一个焦点的距离为()- A.2
- B.3
- C.5
- D.7
-
已知集合
 ,则
,则 等于()
等于()- A.

- B.

- C.

- D.

- A.
-
函数
 和
和 在同一直角坐标系内的图像可以是()
在同一直角坐标系内的图像可以是()- A.

- B.

- C.

- D.

- A.




