高职单招数学模拟试题(4)

设等差数列的前n项数和为S_n、已知的通项公式及它的前n项和T_n.

如图，四棱锥P-ABCD中，PA丄底面ABCD，AB//CD，AD=CD=1，BAD=120°，PA=，ACB=90°。

（1）求证：BC丄平面PAC。

（2）求点B到平面PCD的距离。

某篮球运动员进行投篮测验，每次投中的概率是0.9，假设每次投篮之间没有影响，

（1）求该运动员投篮三次都投中的概率

（2）求该运动员投篮三次至少一次投中的概率

已知函数.

（1） 求f（x）的定义域；

（2） 判断f（x）的奇偶性，并加以证明！

（3） a＞1时，判断函数的单调性并加以证明。

已知A，B分别是椭圆的左右两个焦点。o为坐标的原点，点P（－1，）在椭圆上，线段PB与y轴的焦点M为线段PB的中心点，求椭圆的标准方程

若α，β是二次方程的两个实根，求当m取什么值时，取最小值，并求出此最小值

已知抛物线y²=4x与直线y=2x+b相交与A，B两点，弦长为，求b的值。

若展开式中各项系数的和为128，则展开式中x²项的系数为_____.

若函数_____.

五位同学站成一排，其中甲既不站在排头也不站在排尾的排法有_____种.

拋物线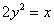的焦点坐标是_____.

已知函数，若f（x）=2，则x=_____.

已知互为反函数，则k和b的值分别是（）

• A.2，
• B.2，
• C.-2，
• D.-2，

下列各组数中成等比数列的是（)

• A.
• B.
• C.4，8，12
• D.

设平面向量a（3，5）b（-2，1），则a-2b的坐标是（）

• A.（7，3）
• B.（-7，-3）
• C.（-7，3）
• D.（7，-3）

设集合，，则（）

• A.A，B的都是有限集
• B.A，B的都是无限集
• C.A是有限集，B是无限集
• D.B是有限集，A是无限集

在ABC中，C=45°，则（1-tanA）（1-tanB）=（）

• A.1
• B.-1
• C.2
• D.-2

从1，2，3，4，5这5个数中，任取四个上数组成没有重复数字的四为数，其中5的倍数的概率是（）

• A.
• B.
• C.
• D.

（x+2）⁶的展开式中x⁴的系数是（）

• A.20
• B.40
• C.60
• D.80

函数在（-，3）上单调递增，则a的取值范围是（）

• A.a≥6
• B.a≤6
• C.a＞6
• D.-8

若是两条不重合的直线表示平面，给出下列正确的个数（）

（1）

（2）

（3）

（4）

• A.l
• B.2
• C.3
• D.4

AB＞0是a＞0且b＞0的（）

• A.充分条件
• B.必要条件
• C.充要条件
• D.既不充分也不必要条件