2013年全国硕士研究生考试《数学》(二)真题及答案
-
设二次型
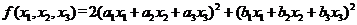
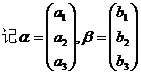
(1)证明二次型f对应的矩阵为
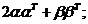 若
若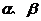 .
.(2)
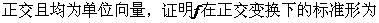
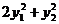 .
. -
设曲线L的方程为
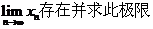
(1)求L的弧长。
(2)设D是由曲线L,直线x=1,x=e及x轴所围平面图形,求D的形心的横坐标.
-
设
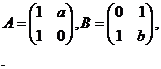
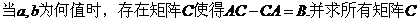 。
。 -
求曲线

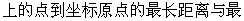 短距离.
短距离. -
设函数
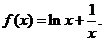
(1)求f(x)的最小值.
(2)设数列{xn}满足
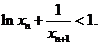 证明
证明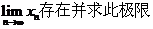 。
。 -
设奇函数f(x)在[-1,1]上具有二阶导数,且f(1)=1.证明:
(1)存在
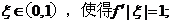
(2)存在
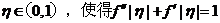 。
。 -
设D是由曲线
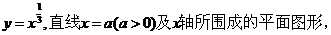
 绕x轴,y轴旋转一周所得旋转体的体积,若Vy=10Vx,求a的值
绕x轴,y轴旋转一周所得旋转体的体积,若Vy=10Vx,求a的值 -
设平面区域D由直线x=3y,y=3xRx+y=8围成.计算
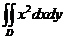
-
当
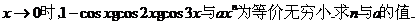
-
设A=
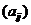 是3阶非零矩阵,|A|为A的行列式,Aij为
是3阶非零矩阵,|A|为A的行列式,Aij为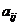 的代数余子式,若
的代数余子式,若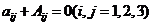 ,则|A|=______________
,则|A|=______________ -
曲线
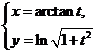 上对应于t=1的点处的法线方程为____________
上对应于t=1的点处的法线方程为____________ -
已知
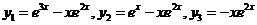 是某二阶常系数非齐次线性微分方程的3个解,则该方程满足条件
是某二阶常系数非齐次线性微分方程的3个解,则该方程满足条件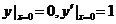 的解为y=__________
的解为y=__________ -
设函数
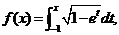 则y=f(x)的反函数
则y=f(x)的反函数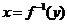 在
在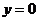 处的导数
处的导数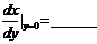
-
设封闭曲线L的极坐标方程为
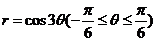 ,则L所围平面图形的面积是
,则L所围平面图形的面积是 -
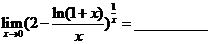
-
矩阵
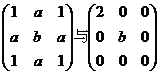 相似的充分必要条件为( )
相似的充分必要条件为( )- A.a=0,b=2
- B.a=0,b为任意常数
- C.a=2,b=0
- D.a=2,b为任意常数
-
设A、B、C均为n阶矩阵,若AB=C,且B可逆,则
- A.矩阵C的行向量组与矩阵A的行向量组等价
- B.矩阵C的列向量组与矩阵A的列向量组等价
- C.矩阵C的行向量组与矩阵B的行向量组等价
- D.矩阵C的列向量组与矩阵B的列向量组等价
-
设
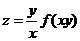 ,其中函数f可微,则
,其中函数f可微,则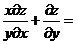 ( )
( )- A.
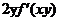
- B.
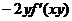
- C.
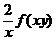
- D.
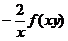
- A.
-
设
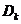 是圆域
是圆域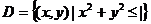 在第k象限的部分,记
在第k象限的部分,记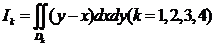 ,则( )
,则( )- A.
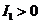
- B.

- C.

- D.
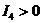
- A.
-
设函数f(x)=
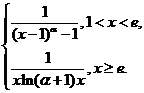 若反常积分
若反常积分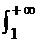 f(x)dx收敛,则( )
f(x)dx收敛,则( )- A.
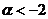
- B.
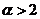
- C.
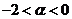
- D.
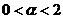
- A.
-
设函数f(x)=
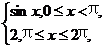 F(x)=
F(x)=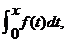 则( )
则( )- A.x=
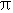 是函数F(x)的跳跃间断点
是函数F(x)的跳跃间断点 - B.x=
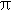 是函数F(x)的可去间断点
是函数F(x)的可去间断点 - C.F(x)在x=
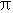 处连续但不可导
处连续但不可导 - D.F(x)在x=
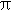 处可导
处可导
- A.x=
-
设cosx-1=xsina(x),其中|a(x)|<
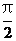 ,则当x→0时,a(x)是( )
,则当x→0时,a(x)是( )- A.比x高阶的无穷小
- B.比x低阶的无穷小
- C.与x同阶但不等价的无穷小
- D.与x等价的无穷小
-
设函数y=f(x)由方程cos(xy)+lny-x=1确定,则
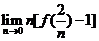 =( )
=( )- A.2
- B.1
- C.-1
- D.-2
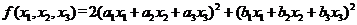
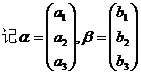
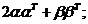 若
若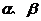 .
.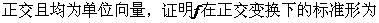
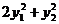 .
.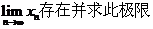
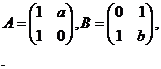
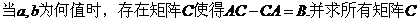 。
。
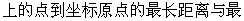 短距离.
短距离.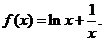
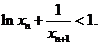 证明
证明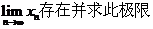 。
。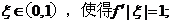
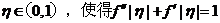 。
。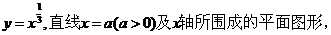
 绕x轴,y轴旋转一周所得旋转体的体积,若Vy=10Vx,求a的值
绕x轴,y轴旋转一周所得旋转体的体积,若Vy=10Vx,求a的值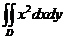
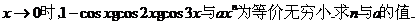
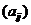 是3阶非零矩阵,|A|为A的行列式,Aij为
是3阶非零矩阵,|A|为A的行列式,Aij为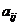 的代数余子式,若
的代数余子式,若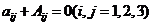 ,则|A|=______________
,则|A|=______________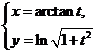 上对应于t=1的点处的法线方程为____________
上对应于t=1的点处的法线方程为____________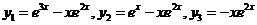 是某二阶常系数非齐次线性微分方程的3个解,则该方程满足条件
是某二阶常系数非齐次线性微分方程的3个解,则该方程满足条件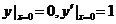 的解为y=__________
的解为y=__________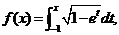 则y=f(x)的反函数
则y=f(x)的反函数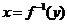 在
在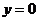 处的导数
处的导数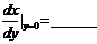
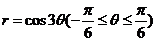 ,则L所围平面图形的面积是
,则L所围平面图形的面积是 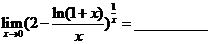
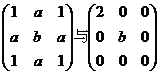 相似的充分必要条件为( )
相似的充分必要条件为( )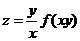 ,其中函数f可微,则
,其中函数f可微,则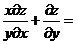 ( )
( )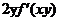
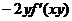
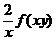
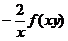
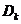 是圆域
是圆域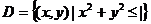 在第k象限的部分,记
在第k象限的部分,记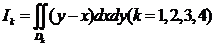 ,则( )
,则( )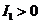

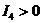
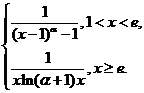 若反常积分
若反常积分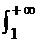 f(x)dx收敛,则( )
f(x)dx收敛,则( )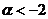
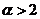
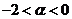
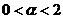
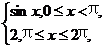 F(x)=
F(x)=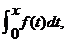 则( )
则( )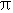 是函数F(x)的跳跃间断点
是函数F(x)的跳跃间断点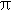 是函数F(x)的可去间断点
是函数F(x)的可去间断点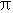 处连续但不可导
处连续但不可导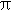 处可导
处可导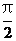 ,则当x→0时,a(x)是( )
,则当x→0时,a(x)是( )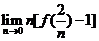 =( )
=( )