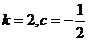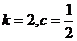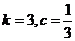2013年全国硕士研究生考试《数学》(一)真题及答案
-
设总体X的概率密度为
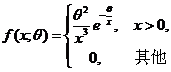 其中
其中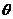 为未知参数且大于零,
为未知参数且大于零,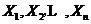 为来自总体X的简单随机样本。(1)>求
为来自总体X的简单随机样本。(1)>求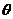 的矩估计量;
的矩估计量;(2)求
 的最大似然估计量。
的最大似然估计量。 -
设二次型
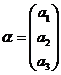 ,记
,记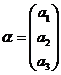 ,
,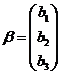 。(1)证明二次型f对应的矩阵为
。(1)证明二次型f对应的矩阵为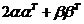 ;
;(2)若
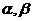 正交且均为单位向量,证明f在正交变换下的标准形为
正交且均为单位向量,证明f在正交变换下的标准形为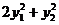 。
。 -
设随机变量X的概率密度为
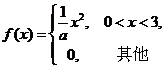 令随机变量
令随机变量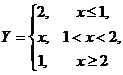 (1)求Y的分布函数;
(1)求Y的分布函数;(2)求概率
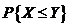 .
. -
设奇函数f(x)在
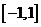 上具有二阶导数,且f(1)=1,证明:
上具有二阶导数,且f(1)=1,证明:(I)存在
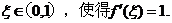
(Ⅱ)存在
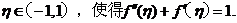
-
设
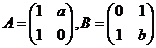 ,当a,b为何值时,存在矩阵C使得AC-CA=B,并求所有矩阵C。
,当a,b为何值时,存在矩阵C使得AC-CA=B,并求所有矩阵C。 -
设直线L过A(1,0,0),B(0,1,1)两点将L绕z轴旋转一周得到曲面
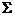 ,
,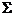 与平面
与平面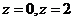 所围成的立体为
所围成的立体为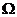 。(1)求曲面
。(1)求曲面 的方程;
的方程;(2)求
 的形心坐标。
的形心坐标。 -
设数列{an}满足条件:
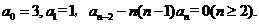 S(x)是幂级数
S(x)是幂级数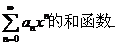
(1)证明:
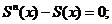
(2)求
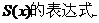
-
求函数
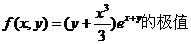 .
. -
计算
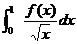 ,其中f(x)=
,其中f(x)=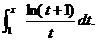
-
设A=(aij)是3阶非零矩阵,
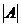 为A的行列式,Aij为aij的代数余子式.若aij+Aij=0(i,j=1,2,3),则|A|=____。
为A的行列式,Aij为aij的代数余子式.若aij+Aij=0(i,j=1,2,3),则|A|=____。 -
设随机变量Y服从参数为1的指数分布,a为常数且大于零,则P{Y≤a+1|Y>a}=
-
设
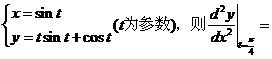 ____。
____。 -
 ____。
____。 -
已知y1=e3x–xe2x,y2=ex–xe2x,y3= –xe2x是某二阶常系数非齐次线性微分方程的3个解,则该方程的通解y=____。
-
设函数y=f(x)由方程y-x=ex(1-y)确定,则
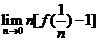 =____ 。
=____ 。 -
设随机变量
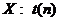 ,
,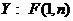 ,给定
,给定 ,常数c满足
,常数c满足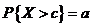 ,则
,则 ( )
( )- A.

- B.
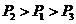
- C.
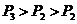
- D.
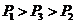
- A.
-
矩阵
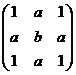 与
与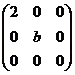 相似的充分必要条件为( )
相似的充分必要条件为( )- A.
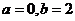
- B.
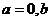 为任意常数
为任意常数 - C.
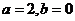
- D.
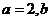 为任意常数
为任意常数
- A.
-
设
 是随机变量,且
是随机变量,且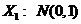 ,
, ,
, ,
,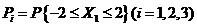 ,则( )
,则( )- A.

- B.
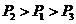
- C.
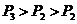
- D.
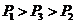
- A.
-
设
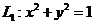 ,
, ,
,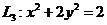 ,
,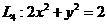 为四条逆时针方向的平面曲线,记
为四条逆时针方向的平面曲线,记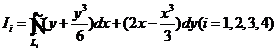 ,则
,则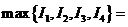
- A.

- B.

- C.
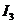
- D.
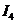
- A.
-
设A,B,C均为n阶矩阵,若AB=C,且B可逆,则( )
- A.矩阵C的行向量组与矩阵A的行向量组等价
- B.矩阵C的列向量组与矩阵A的列向量组等价
- C.矩阵C的行向量组与矩阵B的行向量组等价
- D.矩阵C的列向量组与矩阵B的列向量组等价
-
曲面
 在点
在点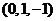 处的切平面方程为( )
处的切平面方程为( )- A.
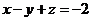
- B.
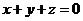
- C.
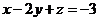
- D.
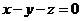
- A.
-
设
 ,
,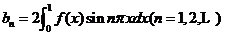 ,令
,令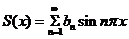 ,则( )
,则( )- A.

- B.
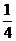
- C.
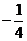
- D.
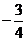
- A.
-
已知极限
 ,其中k,c为常数,且
,其中k,c为常数,且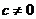 ,则( )
,则( )- A.
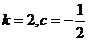
- B.
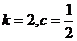
- C.

- D.
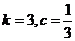
- A.
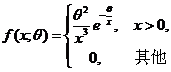 其中
其中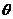 为未知参数且大于零,
为未知参数且大于零,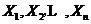 为来自总体X的简单随机样本。(1)>求
为来自总体X的简单随机样本。(1)>求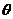 的矩估计量;
的矩估计量; 的最大似然估计量。
的最大似然估计量。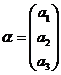 ,记
,记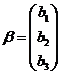 。(1)证明二次型f对应的矩阵为
。(1)证明二次型f对应的矩阵为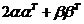 ;
;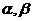 正交且均为单位向量,证明f在正交变换下的标准形为
正交且均为单位向量,证明f在正交变换下的标准形为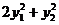 。
。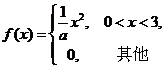 令随机变量
令随机变量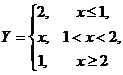 (1)求Y的分布函数;
(1)求Y的分布函数;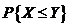 .
.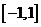 上具有二阶导数,且f(1)=1,证明:
上具有二阶导数,且f(1)=1,证明: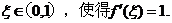
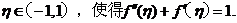
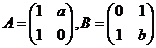 ,当a,b为何值时,存在矩阵C使得AC-CA=B,并求所有矩阵C。
,当a,b为何值时,存在矩阵C使得AC-CA=B,并求所有矩阵C。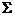 ,
,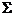 与平面
与平面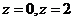 所围成的立体为
所围成的立体为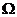 。(1)求曲面
。(1)求曲面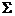 的方程;
的方程;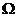 的形心坐标。
的形心坐标。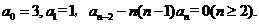 S(x)是幂级数
S(x)是幂级数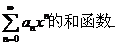
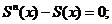
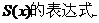
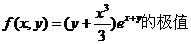 .
.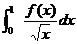 ,其中f(x)=
,其中f(x)=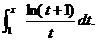
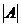 为A的行列式,Aij为aij的代数余子式.若aij+Aij=0(i,j=1,2,3),则|A|=____。
为A的行列式,Aij为aij的代数余子式.若aij+Aij=0(i,j=1,2,3),则|A|=____。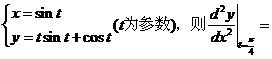 ____。
____。 ____。
____。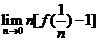 =____ 。
=____ 。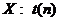 ,
,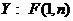 ,给定
,给定 ,常数c满足
,常数c满足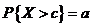 ,则
,则 ( )
( )
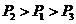
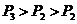
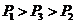
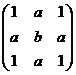 与
与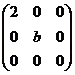 相似的充分必要条件为( )
相似的充分必要条件为( )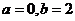
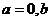 为任意常数
为任意常数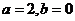
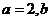 为任意常数
为任意常数 是随机变量,且
是随机变量,且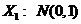 ,
, ,
, ,
,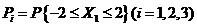 ,则( )
,则( )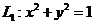 ,
, ,
,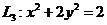 ,
,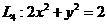 为四条逆时针方向的平面曲线,记
为四条逆时针方向的平面曲线,记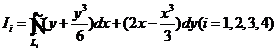 ,则
,则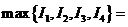


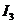
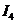
 在点
在点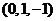 处的切平面方程为( )
处的切平面方程为( )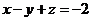
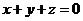
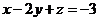
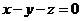
 ,
,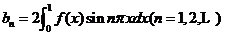 ,令
,令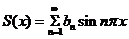 ,则( )
,则( )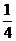
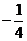
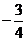
 ,其中k,c为常数,且
,其中k,c为常数,且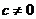 ,则( )
,则( )