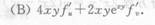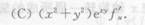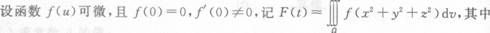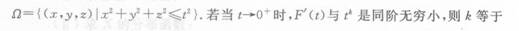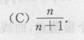2014年考研《数学(一)》冲刺预测试卷(2)
-
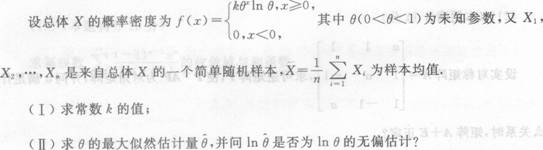
-

-
某人接连不断、独立地对同一目标射击,直到击中为止,以X表示命中时已射击的次 数.假设他共进行了10轮这样的射击,各轮射击的次数分别为1,2,3,4,4,5,3,3,2,3,试求 此人命中率P的矩估计和最大似然估计。
-
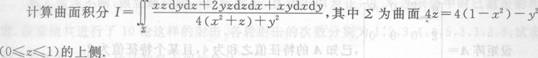
-

-

-

-

-

(I)写出曲线L绕z轴旋转一周所得的曲面∑的方程,并说明∑是何种曲面;
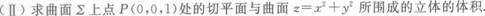
-
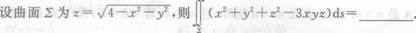 _______
_______ -
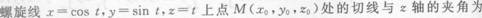
-
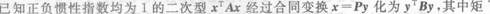
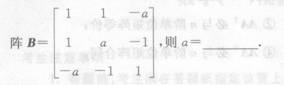
-
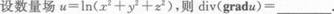
-
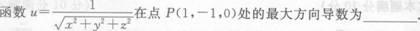
-
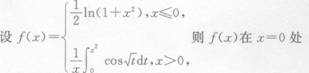

-
设一本书各页的印刷错误的个数X服从泊松分布.已知该书中有一个和两个印刷错误的页数相同,现任意随机抽查3页,则此3页中都没有印刷错误的概率为p=_____.
-
设二次型

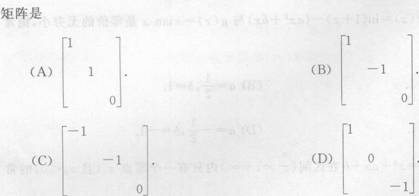
-
设总体X服从正态分布
 是来自总体X的简单随机样本,X为样本均值,若概率
是来自总体X的简单随机样本,X为样本均值,若概率 则a,b满足的关系为
则a,b满足的关系为- A.a=b.
- B.a=2b.
- C.2a=b
- D.a=4b.
-
 是等价的无穷小,则常数a,b的取值为
是等价的无穷小,则常数a,b的取值为
-


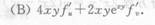
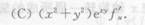

-
设非齐次线性方程组Ax=b无解,则必有
- A.A的行向量组线性无关.
- B.A的行向量组线性相关.
- C.A的列向量组线性无关.
- D.A的列向量组线性相关.
-
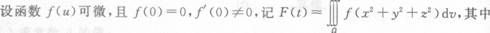
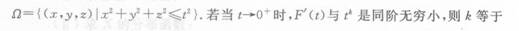
- A.1.
- B.2.
- C.3.
- D.4.
-
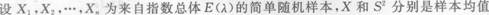

- A.1
- B.2
- C.
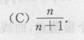
- D.

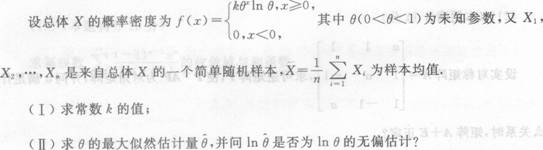

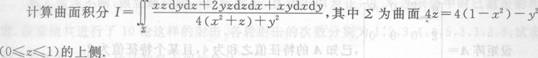





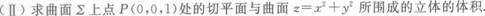
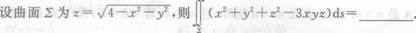 _______
_______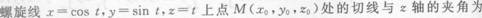
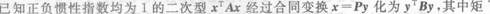

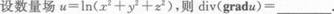
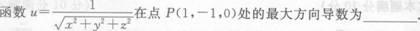
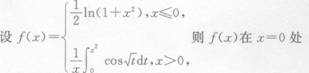


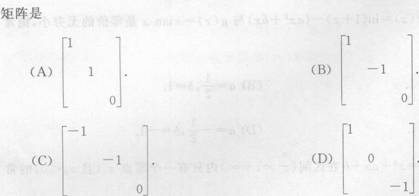
 是来自总体X的简单随机样本,X为样本均值,若概率
是来自总体X的简单随机样本,X为样本均值,若概率 则a,b满足的关系为
则a,b满足的关系为 是等价的无穷小,则常数a,b的取值为
是等价的无穷小,则常数a,b的取值为