自考计算机网络数据结构模拟试卷五

设A和B是两个单链表,其表中元素递增有序。试写一算法将A和B归并成一个按元素值递减有序的单链表C,并要求辅助空间为O(1),请分析算法的时间复杂度。

下面函数 CreateList()的功能是用头插法建立单链表。请在空缺处填写相应的语句

LinkList CreatList()

LinkList head;

ListNode *p;

char ch;

head=NULL;//置空单链表

ch=getchar();//读入第一个字符

while(ch!='\n'){ //读人字符不是结束标志符时作循环

p=(ListNode malloc( sizeof(ListNode));//申请新结点

p->data=   (1)   //数据域赋值

p->next=head;//指针域赋值

   (2)  ;//头指针指向新结点

ch=   (3)  //读入下一个字符

}

return head;//返回链表的头指针

(1)

(2)

(3)

下列函数的功能是:对以带头结点的单链表作为存储结构的两个递增有序表(表中不存在值相同的数据元素)进行如下操作:将所有在Lb表中存在而La表中不存在的结点插入到La中,其中La和Lb分别为两个链表的头指针请在空缺处填人合适内容,使其成为一个完整的算法

void union (LinkList La, LinkList Lb)

{

//本算法的功能是将所有Lb表中存在而La表中不存在的结点插入到La表中

LinkList pre=La,

LinkList pa-La->next;

LinkList pb=Lb->next;

free(Lb);

while (pa &&pb)

{

if (pa->datadata)

pre=pa; pa-pa->next;)

else if (pa->data>pb->data)

{

(1)  ;

pre=pb;

pb=pb->next;

(2)   ;

}

Else

{

q-pb: pb=pb->next; free(q);

}

}

if (pb)

(3)  ;

}

(1)

(2)

(3)

已给如下关于单链表的类型说明:

typedef struct node

int data;

struct node *next;

}listnode, *list;

以下程序采用链表合并的方法,将两个已排序的不带头结点的单链表合并成一个链表而不改变其排序性(升序),这里两个链表的头指针分别为p和q。请将算法补充完整。

void mergelink(list p, list q)

{

list h,;

h=(listnode *)malloc(sizeof(listnode));

h->next=NULL; r=h;

while(p&&q)

if (p->data<=q->data)

(1); r=p: p=p->next;)

else

{(2); r=q; q-q>next;)

if (!p)r->next=q;

if(q)(3);

p=h->next; free();

}

(1)

(2)

(3)

如果希望循环队列中的存储单元都能得到利用,则可设置一个标志域tag,每当尾指针和头指针值相同时,以tag的值为0或1来区分队列状态是“空”还是“满”。请对下列函数填空,使其分别实现与此结构相应的入队列和出队列的算法。

int EnQueue(CirQueue*Q, DataType x)

{

if(Q>tag==)return 0;

Q->data[Q->rear]=;

Q->rear=(Q>rear+1)% QueueSize;

if(-qfront)q→>tag=1

return 1;

}

int DeQueue( CirQueue *, DataType x)

if(  (1)   ) return;

*x-Q->data[Q>front];

Qfront  (2)  

  (3)  ;

return 1;

}

(1)

(2)

(3)

要在[on-1]的向量空间中建立两个栈 stackl和 stack22,请回答

(1)应该如何设计这两个栈才能充分利用整个向量空间?

(2)若的顶指针为topl l, stack的顶指针为top2,如果需要充分利用整个向量空间,则栈 stackl空的条件是:栈 stack2空的条件是:栈 stackI和栈 stack2满的条件是:

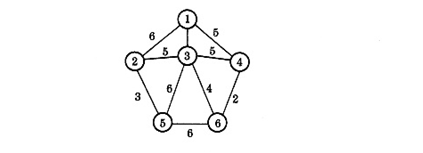
画出题图采用普里姆(Prim)算法构造最小生成树的全过程。

设有序表为(a,b,c,d,e,f,g,i,j,k,p,q),请分别画出对给定值b和n进行折半查找的过程。

(1)画出对表长为13的有序顺序表进行二分查找的判定树。

(2)已知关键字序列为(12,14,16,21,24,28,3,43,52,67,71,84,99),写出在该序列中二分查找37时所需进行的比较次数。

设广义表L(,()),则tail(L)= ( )