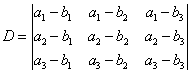线性代数(经管类)2016年10月真题试题及答案解析(04184)
部分试题预览
相关试卷
2019年4月外刊经贸知识选读真题试
所属类型:真题考试2021-03-24
外刊经贸知识选读2008年7月真题试
所属类型:真题考试2021-03-24
外刊经贸知识选读2009年4月真题试
所属类型:真题考试2021-03-24
外刊经贸知识选读2009年7月真题试
所属类型:真题考试2021-03-24
外刊经贸知识选读2010年4月真题试
所属类型:真题考试2021-03-24
外刊经贸知识选读2010年7月真题试
所属类型:真题考试2021-03-24
外刊经贸知识选读2011年4月真题试
所属类型:真题考试2021-03-24
外刊经贸知识选读2011年7月真题试
所属类型:真题考试2021-03-24
外刊经贸知识选读2012年4月真题试
所属类型:真题考试2021-03-24
外刊经贸知识选读2012年7月真题试
所属类型:真题考试2021-03-24
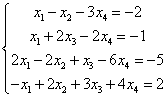 的一个通解。
的一个通解。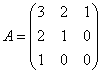 ,求A*及A-1.
,求A*及A-1.